Question

已知抛物线C：y=x²-（m+1）x+1的顶点在坐标轴上．
（1）求m的值；
（2）m＞0时，抛物线C向下平移n（n＞0）个单位后与抛物线C₁：y=ax²+bx+c关于y轴对称，且C₁过点（n，3），求C₁的函数关系式；
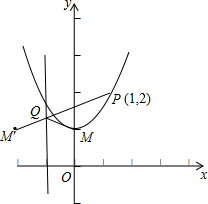
（3）-3＜m＜0时，抛物线C的顶点为M，且过点P（1，y₀）．问在直线x=-1上是否存在一点Q使得△QPM的周长最小，如果存在，求出点Q的坐标，如果不存在，请说明理由．

Answer 1

分析：（1）当抛物线C的顶点在x轴上时，△=[-（m+1）]²-4=0，求出m的值，当抛物线C的顶点在y轴上时，-（m+1）=0，求出m的值，即可得到答案；
（2）当m＞0时，m=1，即可得到抛物线C的解析式，向下平移n（n＞0）个单位后得到y=x²-2x+1-n，根据抛物线y=x²-2x+1-n与抛物线C₁：y=ax²+bx+c关于y轴对称，得到抛物线C₁：y=x²+2x+1-n，把点（n，3）代入求出即可；
（3）存在，根据已知可求出抛物线C的解析式是y=x²+1，把P的坐标代入即可求出P的坐标，作点M（0，1）关于直线x=-1的对称点M′（-2，1），设直线PM′的解析式为y=kx+b，把P、M′的坐标代入得到方程组，求出方程组的解即可求出Q的坐标．

解答：（1）解：当抛物线C的顶点在x轴上时，△=[-（m+1）]²-4=0，
解得m=1或m=-3，
当抛物线C的顶点在y轴上时，-（m+1）=0，
∴m=-1，
即：m=±1或m=-3，
答：m的值是m=±1或m=-3．

（2）解：当m＞0时，m=1，
抛物线C的解析式为y=x²-2x+1，
向下平移n（n＞0）个单位后得到y=x²-2x+1-n，
抛物线y=x²-2x+1-n与抛物线C₁：y=ax²+bx+c关于y轴对称，
∴a=1，b=2，c=1-n，
∴抛物线C₁：y=x²+2x+1-n，
∵抛物线C₁过点（n，3）
∴n²+2n+1-n=3，即n²+n-2=0，
解得n₁=1，n₂=-2（由题意n＞0，舍去）∴n=1
∴抛物线C₁：y=x²+2x，
答：C₁的函数关系式是y=x²+2x．

（3）解：存在，理由是：
当-3＜m＜0时m=-1，
抛物线C的解析式是y=x²+1，
顶点M（0，1），
∵过点P（1，y₀），
∴y₀=1+1=2，
∴P（1，2），
作点M（0，1）关于直线x=-1的对称点M′（-2，1），
设直线PM′的解析式为y=kx+b，
把P（1，2），M′（-2，1）代入得：

2=k+b 1=-2k+b

，
解得：

k= 1 3 b= 5 3

，
∴直线PM′的解析式为y=

1

3

x+

5

3

，
∴Q(-1，

4

3

)，
答：在直线x=-1上存在一点Q，使得△QPM的周长最小，点Q的坐标是（-1，

4

3

）．

点评：本题主要考查对用待定系数法求一次函数的解析式，二次函数图象上点的坐标特征，解一元一次方程，解二元一次方程组，二次函数关于Y轴的点的坐标，平移的性质等知识点的理解和掌握，综合运用这些性质进行计算是解此题的关键，此题是一个综合性很强的题目，题型较好，难度适中．