
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,矩形DEFG的顶点G与△ABC的顶点C重合,边GD、GF分别与AC,BC重合。GD=12,GF=16,矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动,点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点H,矩形DEFG、点Q同时出发,当点Q到达点A时停止运动,矩形DEFG也随之停止运动。设矩形DEFG、点Q运动的时间是t秒(t>0)。(1)求线段DF的长;
(2)求运动过程中,矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式(写出自变量的取值范围);
(3)射线QK能否把矩形DEFG分成面积相等的两部分?若能,求出t值,若不能,说明理由;
(4)连接DH,当DH∥AB时,请直接写出t值。

(1)连接DF,在Rt△CDF中,CD=12,CF=16,根据勾股定理:
DF=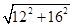 =20
=20
(2)①当0<t ≤2时,s=12×16=192
②当2<t <6时,设矩形DEFG的边EF交AB于点M,边DE交AB于点N
∵ BF=24-4t tanB=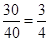
∴MF=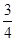 (24-4t)=18-3t
EM=3t-6 NE=
(24-4t)=18-3t
EM=3t-6 NE= EM=4t-8
EM=4t-8
∴s=192-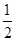 EM.EN=192-6
EM.EN=192-6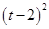
③当6≤t≤10时,设DG与AB交于点M,BF=40- 4t
s=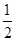 MF.FB=
MF.FB=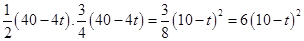
(3)能,当QK经过矩形DEFG的对称中心O时,就可以把矩形DEFG分成面积相等的两部分;
∵在Rt△CDF与Rt△CAB中, ∠C=90°
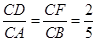
∴Rt△CDF∽Rt△CAB ∴∠CFD=∠B ∴DF∥AB
DF=20,
OF=10 BF=24-4t HF=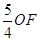 =
=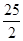 QB=5t
QB=5t
∴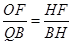

t=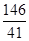
(4)
t=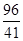
【解析】(1)由勾股定理即可求出DF的长;
(2)分0<t ≤2,2<t <6,6≤t≤10三种情况进行讨论;
(3)连接DF,过点F作FH⊥AB于点H,由四边形CDEF为矩形,QK把矩形CDEF分为面积相等的两部分,根据△HBF∽△CBA,对应边的比相等,就可以求得t的值;
(4)当PG∥AB时四边形PHQG是矩形,由此可以直接写出t.


科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com