

分析 (1)连接AA′,根据折叠的性质得到∠DAE=∠DA′E,根据三角形的外角的性质计算即可;
(2)与(1)的证明过程类似,证明即可;
(3)根据折叠的性质和三角形内角和定理解答即可.
解答 解:(1)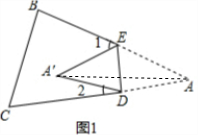 如图1,连接AA′.
如图1,连接AA′.
则△A′ED即为折叠前的三角形,
由折叠的性质知:∠DAE=∠DA′E.
由三角形的外角性质知:
∠1=∠EAA′+∠EA′A,∠2=∠DAA′+∠DA′A;
则∠1+∠2=∠DAE+∠DA′E=2∠DAE,
即∠1+∠2=2∠A,
则∠A=35°;
(2)连接AA′.
则△A′ED即为折叠前的三角形,
由折叠的性质知:∠DAE=∠DA′E.
由三角形的外角性质知:
∠1=∠EAA′+∠EA′A,∠2=∠DAA′+∠DA′A;
则∠1+∠2=∠DAE+∠DA′E=2∠DAE,
即∠1+∠2=2∠A,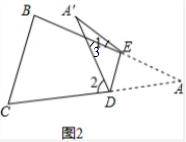
故答案是:∠1+∠2=2∠A;
(3)∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,
∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°,
整理得,2∠A=∠2-∠1.
∴∠A=$\frac{1}{2}$(∠1-∠2).
故答案为:∠A=$\frac{1}{2}$(∠1-∠2).
点评 本题考查的是三角形的外角性质和图形的翻折变换,理清图中角与角的关系是解决问题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com