
【题目】如图,在平面直角坐标系中有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。
。
(1)请直接写出![]() 点坐标。
点坐标。
(2)将![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,
个单位, ![]() 、
、![]() 两点的对应点、正好落在反比例函数
两点的对应点、正好落在反比例函数![]() 在第一象限内图象上。请求出
在第一象限内图象上。请求出![]() ,
, ![]() 的值。
的值。
(3)在(2)的条件下,问是否存![]() 轴上的点
轴上的点![]() 和反比例函数
和反比例函数![]() 图象上的点
图象上的点![]() ,使得以
,使得以![]() 、
、![]() ,
, ![]() ,
, ![]() 为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点
为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点![]() 和点
和点![]() 的坐标;如果不存在,请说明理由。
的坐标;如果不存在,请说明理由。

【答案】(1) ![]() 点坐标为(-4,3);
点坐标为(-4,3);
(2) ![]() 的值为6,
的值为6, ![]() 的值为6;
的值为6;
(3)M的坐标为(6.5,0)N的坐标为(1.5,4),或M的坐标为(7,0)N的坐标为(3,2),或M的坐标为(-7,0)N的坐标为(-3,2)
【解析】试题分析:(1)由在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,可证得△ADC≌△BOA,继而求得C点坐标;
(2)![]() 向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),由B′、C′正好落在反比例函数
向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),由B′、C′正好落在反比例函数![]() 的图象上,即可得t=2(t-3),继而求得t的值,则可求得k的值 ;
的图象上,即可得t=2(t-3),继而求得t的值,则可求得k的值 ;
(3)进行分类试论出MN的位置,即可得解.
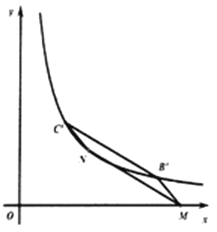
试题解析:(1)如图1,过点C作CD⊥x轴于点D,则∠ADC=∠AOB=90°,
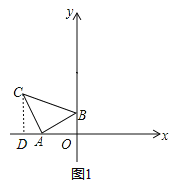
∴∠DAC+∠ACD=90°,
∵Rt△ABC,∠A=90°,
∴∠DAC+∠BAO=90°,
∴∠BAO=∠ACD,
在△ADC和△BOA中,
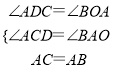 ,
,
∴△ADC≌△BOA(AAS),
∴AD=OB=1,CD=OA=3,
∴OD=OA+AD=4,
∴C点坐标为:(-4,2);
(2)ΔABC向右平移了t个单位长度,则点B′的坐标为(t,1)、C′的坐标为(t-3,2),如图,
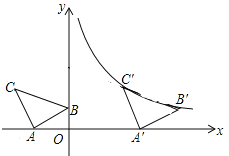
∵B′、C′正好落在反比例函数![]() 图象上,
图象上,
∴t=2(t-3),
解得:t=6,
∴B′(6,1),C′(3,2),
∴k=6;
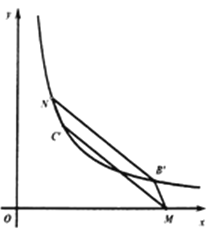
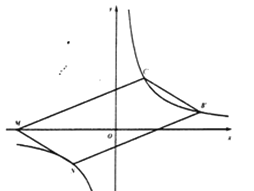
(3)MN平行四边形MCˊNBˊ对角线时,由平行四边形对错爱线互相平分,可知线段BˊCˊ,MN的中点为同一个点,即: ![]() ,yN =4,代入
,yN =4,代入![]() ,得xN=1.5
,得xN=1.5
故N点坐标为(1.5,4)
![]() ,xN=6.5,所以M点的坐标为(6.5,0)
,xN=6.5,所以M点的坐标为(6.5,0)
MCˊ平行四边形MNCˊBˊ对角线时,可得M的坐标为(7,0),N点的坐标为(3,2)
MBˊ平行四边形MCˊBˊN对角线时,可得M的坐标为(-7,0),N点的坐标为(-3,2)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某服装店举办促销活动,促销方法是“原价x元的服装打7折后再减去10元”,则下列代数式中,能正确表达该商店促销方法的是( )
A. 30%(x﹣10) B. 30%x﹣10 C. 70%(x﹣10) D. 70%x﹣10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】氢原子的半径大约是0.000 0077m,将数据0.000 0077用科学记数法表示为( )
A. 0.77×10﹣5 B. 0.77×10﹣6 C. 7.7×10﹣5 D. 7.7×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程x2﹣4x+m+1=0有两个不相等的实数根.
(1)求m的取值范围;(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
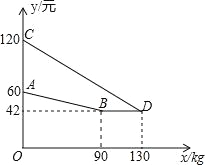
(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com