
【题目】如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.
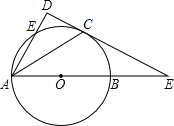
(1)求证:DC为⊙O切线;
(2)若DC=1,AC=![]() ,①求⊙O半径长;②求PB的长.
,①求⊙O半径长;②求PB的长.
【答案】(1)见解析;(2)⊙O半径长为![]() ;
;
【解析】
试题分析:(1)连结OC,如图,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于CD⊥AD,所以OC⊥CD,则根据切线的判定定理得到DC为⊙O切线;
(2)①连结BC,如图,在Rt△ACD中利用勾股定理计算出AD=2,再Rt△ACD∽Rt△ABC,利用相似比计算出AB=![]() ,从而得到⊙O半径长为
,从而得到⊙O半径长为![]() ;
;
②证明△EOC∽△EAD,然后利用相似比可计算出BE的长.
(1)证明:连结OC,如图,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥CD,
∴DC为⊙O切线;
(2)解:①连结BC,如图,
在Rt△ACD中,∵CD=1,AC=![]() ,
,
∴AD=![]() =2,
=2,
∵AB为直径,
∴∠ACB=90°,
∵∠1=∠2,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,即![]() :AB=2:
:AB=2:![]() ,
,
∴AB=![]() ,
,
∴⊙O半径长为![]() ;
;
②∵OC∥AD,
∴△EOC∽△EAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,AB与CD不平行,AC与BD相交于点O,那么下列条件中能判定四边形ABCD是等腰梯形的是( )
A. AC=BD=BC B. AB=AD=CD C. OB=OC,AB=CD D. OB=OC,OA=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
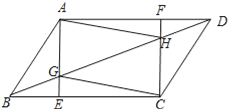
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com