
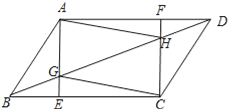
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
【答案】证明见解析.
【解析】法1:由平行四边形对边平行,且CF与AD垂直,得到CF与BC垂直,根据AE与BC垂直,得到AE与CF平行,得到一对内错角相等,利用等角的补角相等得到∠AGB=∠DHC,根据AB与CD平行,得到一对内错角相等,再由AB=CD,利用AAS得到三角形ABG与三角形CDH全等,利用全等三角形对应边相等得到AG=CH,利用一组对边平行且相等的四边形为平行四边形即可得证;
法2:连接AC,与BD交于点O,利用平行四边形的对角线互相平分得到OA=OC,OB=OD,再由AB与CD平行,得到一对内错角相等,根据CF与AD垂直,AE与BC垂直,得一对直角相等,利用ASA得到三角形ABG与三角形CDH全等,利用全等三角形对应边相等得到BG=DH,根据等式的性质得到OG=OH,利用对角线互相平分的四边形为平行四边形即可得证.
证明:在□ABCD中,AD∥BC,AB∥CD,
∵CF⊥AD,∴CF⊥BC,
∵AE⊥BC,∴AE∥CF,即AG∥CH,∴∠AGH=∠CHG,
∵∠AGB=180°﹣∠AGH,∠DHC=180°﹣∠CHG,
∴∠AGB=∠DHC,
∵AB∥CD,∴∠ABG=∠CDH,∴△ABG≌CDH,
∴AG=CH,
∴四边形AGCH是平行四边形;
法2:连接AC,与BD相交于点O,
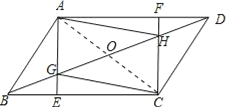

在□ABCD中,AO=CO,BO=DO,∠ABE=∠CDF,AB∥CD,
∴∠ABG=∠CDH,
∵CF⊥AD,AE⊥BC,
∴∠AEB=∠CFD=90°,
∴∠BAG=∠DCH,
∴△ABG≌CDH,
∴BG=DH,
∴BO﹣BG=DO﹣DH,
∴OG=OH,
∴四边形AGCH是平行四边形.
“点睛”此题考查了平行四边形的判定与性质,熟练掌握平式子变形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
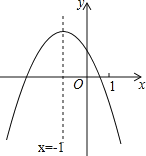
①b2﹣4ac>0;
②4a+c>2b;
③(a+c)2>b2;
④x(ax+b)≤a﹣b.
其中正确结论的是 .(请把正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 (辆) | 借车数 (辆) | 存量y (辆) |
6:00﹣7:00 | 1 | 45 | 5 | 100 |
7:00﹣8:00 | 2 | 43 | 11 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:

(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.
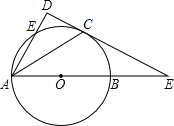
(1)求证:DC为⊙O切线;
(2)若DC=1,AC=![]() ,①求⊙O半径长;②求PB的长.
,①求⊙O半径长;②求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康!你知道吗,即使被动吸烟也大大危害健康、有消息称,我国准备从2011年元月一日起在公众场所实行“禁烟”,为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下统计图:
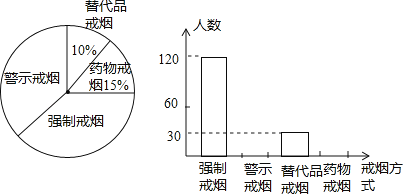
根据统计图解答:
(1)同学们一共随机调查了多少人?
(2)请你把统计图补充完整;
(3)如果在该社区随机咨询一位市民,那么该市民支持“强制戒烟”的概率是多少?假定该社区有1万人,请估计该地区大约有多少人支持“警示戒烟”这种方式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com