
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
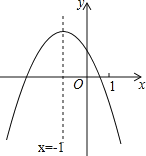
①b2﹣4ac>0;
②4a+c>2b;
③(a+c)2>b2;
④x(ax+b)≤a﹣b.
其中正确结论的是 .(请把正确结论的序号都填在横线上)
【答案】①②④
【解析】
试题分析:①根据抛物线与x轴有两个交点进行判断即可;
②根据当x=﹣2时,y>0判断即可;
③根据x=﹣1时,y>0可知a﹣b+c>0,判断即可;
④根据x=﹣1时,y有最大值a﹣b+c判断即可.
解:①∵抛物线与x轴由两个交点,
∴b2﹣4ac>0,
①正确;
②由图象可知,当x=﹣2时,y>0,
即4a﹣2b+c>0,
∴4a+c>2b,
②正确;
③∵x=﹣1时,y>0,
∴a﹣b+c>0,
∴a+c>b,
∵a+b+c<0,∴a+c<﹣b,
∴(a+c)2<b2,
③错误;
④∵x=﹣1时,y有最大值a﹣b+c,
∴ax2+bx+c≤a﹣b+c,
∴x(ax+b)≤a﹣b,
④正确.
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
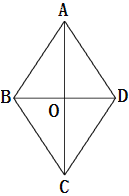
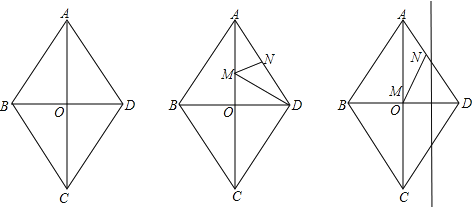
【题目】如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4).连接OA,
线段OA长______; (2)若在直线a上存在点P,使△AOP是以OA为腰的等腰三角形.那么所有满足条件的点P的坐标是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“上品”房地产开发公司于2010年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格y1(单位:万元/m2)与月份x(6≤x≤11,x为整数)之间满足一次函数关系:每月的销售面积为y2(单位:m2),其中y2=﹣2000x+26000(6≤x≤11,x为整数).
(1)求y1与月份x的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2010年11月时,因会受到即将实行的“国八条”和房产税政策的影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少20a%,于是决定将12月份的销售价格在11月的基础上增加a%,该计划顺利完成.为了尽快收回资金,2011年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出a的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
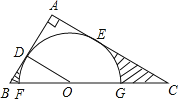
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
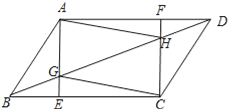
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com