
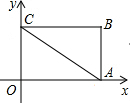
 如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.分析 (1)过O作AC的垂线,截取得到点E,连接CE,AE,交BC于点N,如图所示;
(2)根据矩形OABC,得到对边相等,四个角为直角,再由折叠的性质得到△AOC≌△AEC,利用全等三角形的性质及等量代换得到EC=BA,再由两对角相等,利用AAS即可得证;
(3)由△CEN≌△ABN,得到CN=AN,设CN=AN=x,由BC-CN表示出BN,在直角三角形ABN中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CN的长,即可确定出N的坐标.
解答 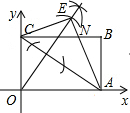 解:(1)如图所示,△ACE为所求的三角形;
解:(1)如图所示,△ACE为所求的三角形;
(2)∵矩形OABC,△AOC沿AC对折得到△AEC,即△AOC≌△AEC,
∴OC=AB=CE=6,BC=OA=AE=8,∠AOC=∠B=∠AEC=90°,
在△CEN和△ABN中,
$\left\{\begin{array}{l}{∠AEC=∠CBA=90°}\\{∠ENC=∠BNA}\\{EC=BA}\end{array}\right.$,
∴△CEN≌△ABN(AAS);
(3)∵△CEN≌△ABN,
∴CN=AN,
设CN=AN=x,则BN=BC-CN=8-x,
在Rt△ABN中,根据勾股定理得:AN2=AB2+BN2,
即x2=62+(8-x)2,
整理得:x2=36+64-16x+x2,
解得:x=$\frac{25}{4}$,
∴CN=$\frac{25}{4}$,
则N的坐标为($\frac{25}{4}$,6).
故答案为:($\frac{25}{4}$,6)
点评 此题属于一次函数综合题,涉及的知识有:折叠的性质,矩形的性质,全等三角形的判定与性质,勾股定理,以及坐标与图形性质,熟练掌握全等三角形的判定与性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a+b)(2a-b)=2a2-b2 | B. | (a+2)(b-1)=ab-2 | C. | (a+1)2=a2+1 | D. | (x-1)(x-2)=x2-3x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线y=-x上 | B. | 直线y=x上 | C. | 双曲线y=$\frac{1}{x}$ | D. | 抛物线y=x2上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
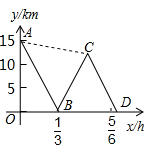 “五一”小长假,小明和妈妈准备乘动车去北京旅游,离火车出发还有一个小时.小明的爸爸骑摩托车想尽快将小明和妈妈俩从家送到汉口火车站.由于摩托车后座只能坐1人,为了节约时间,爸爸骑摩托车先带着小明出发,同时,小明的妈妈也步行出发沿同一路线去火车站.已知小明妈妈步行的速度是5km/h,摩托车的速度是45km/h.爸爸将小明送到车站后,立即回去接妈妈,再将妈妈送到车站.图中折线A-B-C-D、线段AC分别表示爸爸、妈妈在上述过程中,离车站的路程y(km)与爸爸所用时间x(h)之间的函数关系.根据图中的信息可知:当妈妈到达火车站时离火车开车的时间还有10分钟.
“五一”小长假,小明和妈妈准备乘动车去北京旅游,离火车出发还有一个小时.小明的爸爸骑摩托车想尽快将小明和妈妈俩从家送到汉口火车站.由于摩托车后座只能坐1人,为了节约时间,爸爸骑摩托车先带着小明出发,同时,小明的妈妈也步行出发沿同一路线去火车站.已知小明妈妈步行的速度是5km/h,摩托车的速度是45km/h.爸爸将小明送到车站后,立即回去接妈妈,再将妈妈送到车站.图中折线A-B-C-D、线段AC分别表示爸爸、妈妈在上述过程中,离车站的路程y(km)与爸爸所用时间x(h)之间的函数关系.根据图中的信息可知:当妈妈到达火车站时离火车开车的时间还有10分钟.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com