
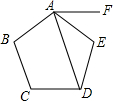
 如图,过正五边形ABCDE的顶点A作AF∥CD,连结AD,则∠FAD=72度.
如图,过正五边形ABCDE的顶点A作AF∥CD,连结AD,则∠FAD=72度.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
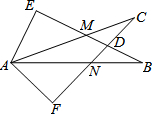 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则$\frac{DE}{EF}$=$\frac{3}{5}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则$\frac{DE}{EF}$=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.
随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.| 组别 | 行驶的里程x(千米) | 频数(台) | 频率 |
| A | x<200 | 18 | 0.15 |
| B | 200≤x<210 | 36 | a |
| C | 210≤x<220 | 30 | |
| D | 220≤x<230 | b | |
| E | x≥230 | 12 | 0.10 |
| 合计 | c | 1.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com