已知关于x的方程(m-1)x2-2mx+m=0有两个不相等的实数根x1、x2,且(x1-x2)2=8,m的值为 ________.

或2
分析:根据一元二次方程的定义及根的判别式△=b
2-4ac>0解得关于m的取值范围;然后由根与系数的关系求得x
1+x
2与x
1•x
2的值,将其代入(x
1-x
2)
2=(x
1+x
2)
2-4x
1•x
2求得m的值.
解答:∵原方程有两个不同的两个实数根,
∴原方程是二次方程,
∴m-1≠0,且判别式△=(-2m)
2-4(m-1)m>0,
解得,m>0且m≠1;
由韦达定理 x
1+x
2=
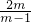
,x
1•x
2=

;
∴(x
1-x
2)
2=(x
1+x
2)
2-4x
1•x
2=8,
即
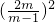
-4×

=8;
设

=t,则t
2-t-2=0,
∴(t+1)(t-2)=0,
∴t+1=0或t-2=0,
∴t=-1,或t=2;
①当t=-1时,

=-1,
解得,m=

(m>0且m≠1);
②当t=2时,

=2,
解得,m=2(m>0且m≠1);
综上所述,m的值为

或2.
故答案为:

或2.
点评:本题考查了一元二次方程根的判别式和根与系数的关系.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

 或2
或2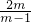 ,x1•x2=
,x1•x2= ;
;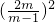 -4×
-4× =8;
=8; =t,则t2-t-2=0,
=t,则t2-t-2=0, =-1,
=-1, (m>0且m≠1);
(m>0且m≠1); =2,
=2, 或2.
或2. 或2.
或2.

 53随堂测系列答案
53随堂测系列答案