
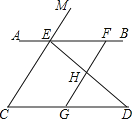
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
【答案】(1)证明见解析;
(2)∠AED+∠D=180°,理由见解析;
(3)∠AEM=130°
【解析】分析:(1)根据同位角相等两直线平行,可证CE∥GF;
(2)根据平行线的性质可得∠C=∠FGD,根据等量关系可得∠FGD=∠EFG,根据内错角相等,两直线平行可得AB∥CD,再根据平行线的性质可得∠AED与∠D之间的数量关系;(3)根据对顶角相等可求∠DHG,根据三角形外角的性质可求∠CGF,根据平行线的性质可得∠C,∠AEC,再根据平角的定义可求∠AEM的度数.
本题解析:(1)证明:∵∠CED=∠GHD, ∴CE∥GF
(2)答:∠AED+∠D=180°
理由:∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD, ∴∠AED+∠D=180°;
(3)∵∠DHG=∠EHF=100°,∠D=30°,
∴∠CGF=100°+30°=130°
∵CE∥GF,∴∠C=180°﹣130°=50°
∵AB∥CD,
∴∠AEC=50°,
∴∠AEM=180°﹣50°=130°.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】用反证法证明:“一个三角形中至多有一个角不小于90°”时,应假设( )
A. 一个三角形中至少有两个角不小于 90°
B. 一个三角形中至多有一个角不小于 90°
C. 一个三角形中至少有一个角不小于 90°
D. 一个三角形中没有一个角不小于 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
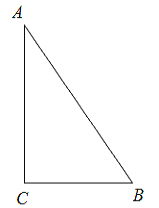
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)问t满足什么条件时,△BCP为直角三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1,2,3,……,100这100个自然数,任意分为50组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,代入代数式![]() 中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
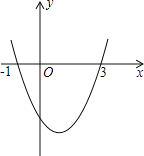
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com