
【题目】在矩形ABCD中,AB=3,BC=6,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C、D的对应点分别为C′、D′,折痕与边AD交于点F,当点B、C′、D′恰好在同一直线上时,AF的长为 .
【答案】4 ![]() 或4﹣
或4﹣ ![]()
【解析】解:由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE, ∵点B、C′、D′在同一直线上,
∴∠BC′E=90°,
∵BC=6,BE=2CE,
∴BE=4,C′E=CE=2,
在Rt△BC′E中, ![]() =2,
=2,
∴∠C′BE=30°,①当点C′在BC的上方时,
如图1,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形,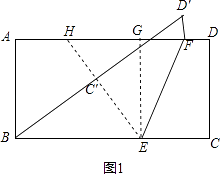
∴EG=AB=3,AG=BE=4,
∵∠C′BE=30°,∠BC′E=90°,
∴∠BEC′=60°,
由折叠的性质得,∠C′EF=′CEF,
∴∠C′EF=∠CEF=60°,
∵AD∥BC,
∴∠HFE=∠CEF=60°,
∴△EFH是等边三角形,
∴在Rt△EFG中,EG=3,
∴GF= ![]() ,
,
∴AF═4+ ![]() ,②当点C′在BC的下方时,如图2,
,②当点C′在BC的下方时,如图2,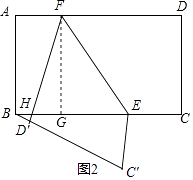
过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形,△EFH是等边三角形,
∴AF=BG,FG=AB=3,∠FEH=60°,
在Rt△EFG中,GE= ![]() ,
,
∵BE=4,
∴BG=4﹣ ![]() ,
,
∴AF=4﹣ ![]() ,
,
综上所述,AF的长是4 ![]() 或4﹣
或4﹣ ![]() .
.
所以答案是:4 ![]() 或4﹣
或4﹣ ![]() .
.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
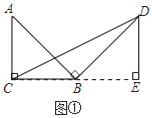
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
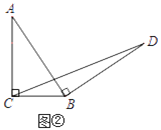
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
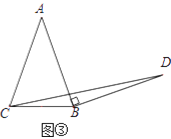
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
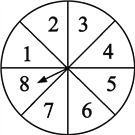
【题目】如图所示,转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.
(1)自由转动转盘,当它停止转动时,指针指向的数正好能整除8的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为![]() .(注:指针指在边缘处,要重新转,直至指到非边缘处)
.(注:指针指在边缘处,要重新转,直至指到非边缘处)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计划拨款9万元从厂家购进50台电视机![]() 已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
![]() 若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
若商场同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下商场的进货方案;
![]() 若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元
若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元![]() 在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案;
![]() 若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
若商场准备用9万元同时购进三种不同的电视机50台,请你设计进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)= ![]() .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)= ![]() .则在以下结论:
.则在以下结论:
①F(5)=5;②F(24)= ![]() ;
;
③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),
则F(a)=x.则正确的结论有________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
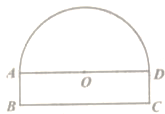
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com