
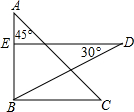
 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )| A. | 内部 | B. | 外部 | C. | 边上 | D. | 以上都有可能 |
分析 先根据勾股定理求出两直角三角形的各边长,再由旋转的性质得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′与直线AB的交点到B的距离也是5$\sqrt{2}$,与AB的值相等,所以点A在△D′E′B的边上.
解答  解:∵AC=BD=10,
解:∵AC=BD=10,
又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5$\sqrt{2}$,
由三角板DEB绕点B逆时针旋转45°得到△D′E′B,设△D′E′B与直线AB交于G,可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴BG=AB,
∴点A在△D′E′B的边上,
故选C.
点评 本题考查了旋转的性质和勾股定理,利用30°和45°的直角三角形的性质求出各边的长;注意:在直角三角形中,30度角所对的直角边等于斜边的一半,45°角所对的两直角边相等,熟练掌握此内容是解决问题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
 被誉为“中国画里乡村”的黄山宏村,村头有一座美丽的圆弧形石拱桥(如图),已知桥拱的顶部C距水面的距离CD为2.7m,桥弧所在的圆的半径OC为1.5m,则水面AB的宽度是( )
被誉为“中国画里乡村”的黄山宏村,村头有一座美丽的圆弧形石拱桥(如图),已知桥拱的顶部C距水面的距离CD为2.7m,桥弧所在的圆的半径OC为1.5m,则水面AB的宽度是( )| A. | 1.8m | B. | 1.6m | C. | 1.2m | D. | 0.9m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
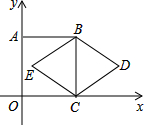 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是(2+$\sqrt{3}$,1).
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是(2+$\sqrt{3}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
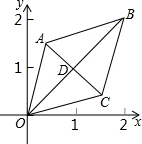 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )| A. | (1,-1) | B. | (-1,-1) | C. | ($\sqrt{2}$,0) | D. | (0,-$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.157×1010 | B. | 1.57×108 | C. | 1.57×109 | D. | 15.7×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com