

分析 (1)n边形的内角和是(n-2)•180°,因而内角和一定是180度的倍数.
(2)多边形的内角一定大于0,并且小于180度,因而内角和再加上一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1.则用内角和于内角的和除以180所得值,加上2,比这个数小的最大的整数就是多边形的边数.
(3)利用多边形的内角和解答即可.
解答 解:(1)因为2013°不是180°的整数倍,所以小明说不可能;
(2)依题意有(x-2)•180°<2013°,
解得x<13$\frac{33}{180}$.
因而多边形的边数是13,该多边形为十三边形.
(3)13边形的内角和是(13-2)×180°=1980°,则错把外角当内角的那个外角的度数是2013°-1980°=33°
点评 此题考查多边形的内角和外角,解决本题的关键是正确记忆运用多边形的内角和公式,是需要熟记的内容.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
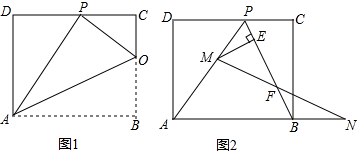
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $y=\frac{3}{4}x-\frac{5}{3}$ | B. | $y=\frac{4}{3}x-\frac{3}{5}$ | C. | $y=\frac{3}{4}x+\frac{3}{5}$ | D. | $y=\frac{4}{3}x-\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
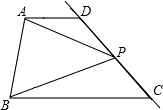 如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).
如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com