
分析 根据题意列出关于x的一元一次不等式$\frac{x+4}{3}$-$\frac{3x-1}{2}$>1,先去分母,然后通过移项、合并同类项、化系数为1进行解答即可.
解答 解:依题意得:$\frac{x+4}{3}$-$\frac{3x-1}{2}$>1,
2x+8-9x+3>6,
-7x>-5,
x<$\frac{5}{7}$.
即当x<$\frac{5}{7}$时,代数式$\frac{x+4}{3}$与$\frac{3x-1}{2}$的差大于1.
点评 本题考查了解一元一次不等式.根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
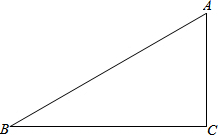 如图,在△ABC中,AB=17,BC=15,AC=8.
如图,在△ABC中,AB=17,BC=15,AC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com