
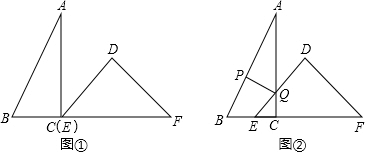
分析 (1)因为点A在线段PQ垂直平分线上,所以得到线段相等,可得CE=CQ,用含t的式子表示出这两个线段即可得解;
(2)由(1)求得CE=CQ=t,AQ=6$\sqrt{3}$-t,AP=12-2t,当∠APQ=90°时,根据cosA=$\frac{AP}{AQ}$列方程解得t=$\frac{24+6\sqrt{3}}{13}$,当∠AQP=90°时,根据cosA=$\frac{AQ}{AP}$得到方程$\frac{6\sqrt{3}-t}{12-2t}$=$\frac{\sqrt{3}}{2}$,此方程无解,于是得到当t=$\frac{24+6\sqrt{3}}{13}$时,△APQ为直角三角形;
(3)过点P作PN⊥BC,垂足为N(如图2),在Rt△PBN中,∠B=60°,BP=2t,由三角函数得到PN=$\sqrt{3}$.求得S△ABC=$\frac{1}{2}$BC•AC=18$\sqrt{3}$,于是得到S四边形APEC=S△ABC-S△PBE=18$\sqrt{3}$-$\frac{1}{2}$(6-t)$•\sqrt{3}$t,=$\frac{\sqrt{3}}{2}$t2-3$\sqrt{3}$t+18$\sqrt{3}$.求出t=3时,S四边形APEC最小,即可得到结果.
解答 解:(1)∵∠ACB=∠EDF=90°,∠BAC=30°,∠DEF=45°,BC=6cm,
∴AB=12cm,AC=6$\sqrt{3}$cm,
依题意,得EC=QC=t.
∴BE=6-t,AQ=6$\sqrt{3}$-t,
∵BP=2t,
∴AP=12-2t.
当点A在线段PQ的垂直平分线上时,AP=AQ,
∴12-2t=6$\sqrt{3}$-t,
解得t=12-6$\sqrt{3}$,
即当t=12-6$\sqrt{3}$时,点A在线段PQ的垂直平分线上;
(2)由(1)求得CE=CQ=t,AQ=6$\sqrt{3}$-t,AP=12-2t,
当∠APQ=90°时,cosA=$\frac{AP}{AQ}$,
∵∠BAC=30°,
∴$\frac{\sqrt{3}}{2}$=$\frac{12-2t}{6\sqrt{3}-t}$,
解得:t=$\frac{24+6\sqrt{3}}{13}$,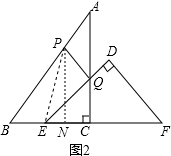
当∠AQP=90°时,cosA=$\frac{AQ}{AP}$,
∴$\frac{6\sqrt{3}-t}{12-2t}$=$\frac{\sqrt{3}}{2}$,
此方程无解,
∴当t=$\frac{24+6\sqrt{3}}{13}$时,△APQ为直角三角形;
(3)过点P作PN⊥BC,垂足为N(如图2),
∵在Rt△PBN中,∠B=60°,BP=2t,
∴PN=$\sqrt{3}$.
∴S△ABC=$\frac{1}{2}$BC•AC=18$\sqrt{3}$,
∴S四边形APEC=S△ABC-S△PBE=18$\sqrt{3}$-$\frac{1}{2}$(6-t)$•\sqrt{3}$t,
=$\frac{\sqrt{3}}{2}$t2-3$\sqrt{3}$t+18$\sqrt{3}$.
∴当t=3时,S四边形APEC最小,
∴此时,BE=6-t=3=CE,PB=2t=6=AP,
∴PE=$\frac{1}{2}$AC=3$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质、二次函数的最值、特殊图形的面积的求法等知识,图形较复杂,考查学生数形结合的能力,综合性强,难度较大,利用已知表示出各线段长度是解题关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 0<x<2 | B. | x<2 | C. | 0<x<3 | D. | x<1或x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
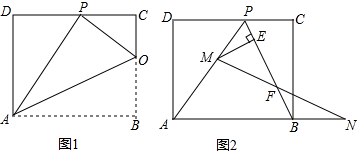
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com