
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
分析 (1)设商场购买甲种商品m件,购买乙种商品n件,根据该商场同时购进甲、乙两种商品共100件,恰好用去2700元列方程组求解即可;
(2)此题可根据“甲、乙两种商品共100件的总利润不少于750元,且不超过760元”列不等式组来求解;
(3)第一天的总价为200元,打折最低应该出270元,所以没有享受打折,第二天的也可能享受了9折,也可能享受了8折.应先算出原价,然后除以单价,得出数量.
解答 解:(1)设商场购买甲种商品m件,购买乙种商品n件,
由题意得:$\left\{\begin{array}{l}{m+n=100}\\{15m+35n=2700}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=40}\\{n=60}\end{array}\right.$.
答:该商场能购进甲种商品40件,乙种商品60件.
(2)设商场购买甲种商品x件,购买乙种商品(100-x)件.
由题意得:750≤(20-15)x+(45-35)(100-x)≤760.
解得:48≤x≤50.
又∵x为非负整数,
∴符合题意的购买方案有3种,分别为:
第一种方案:甲种商品48件,乙种商品52件;
第二种方案:甲种商品49件,乙种商品51件;
第三种方案:甲种商品50件,乙种商品50件.
(3)根据题意得
第一天只购买甲种商品不享受优惠条件,
∴200÷20=10件,
第二天只购买乙种商品有以下两种情况:
情况一:购买乙种商品打九折,324÷90%÷45=8件;
情况二:购买乙种商品打八折,324÷80%÷45=9件.
答:贝贝第一天购买甲种商品10件,第二天购买乙种商品8件或9件.
点评 本题考查了本题考查了二元一次方程组和一元一次不等式组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式组,及所求量的等量关系.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
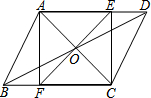 在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:
在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com