
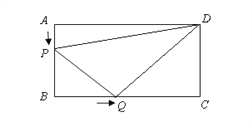
【题目】如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
(1)当PB=2厘米时,求点P移动多少秒?
(2)t为何值时,△PBQ为等腰直角三角形?
(3)求四边形PBQD的面积,并探究一个与计算结果有关的结论.
【答案】(1)4;(2)2;(3)36,不论P、Q怎样运动总有四边形PBQD的面积等于长方形ABCD面积的一半
【解析】试题分析:(1)由AB、PB的长可求得AP的长,则可求得t的值;
(2)根据等腰直角三角形的性质可求得PB=BQ,则可得到关于t的方程,可求得t的值;
(3)可用t分别表示出S△APD、S△QCD,再利用面积的和差可求得四边形PBQD的面积,则可求得结论.
试题解析:
(1)∵PB=2cm,AB=6cm,
∴AP=AB-PB=6-2=4(秒),
即点P移动4秒;
(2)∵△PBQ为等腰直角三角形,
∴PB=BQ,即6-t=2t,解得t=2,
∴当t的值为2秒时,△PBQ为等腰直角三角形;
(3)由题意可知AP=t,AB=6,BQ=2t,BC=12,
∴PB=6-t,QC=12-2t,CD=6,AD=12,
∴S△APD=![]() APAD=
APAD=![]() t×12=6t,
t×12=6t,
S△QCD=![]() QCCD=
QCCD=![]() (12-2t)6=36-6t,
(12-2t)6=36-6t,
∴S四边形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36,
结论:不论P、Q怎样运动总有四边形PBQD的面积等于长方形ABCD面积的一半.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
知识运用:
(1)如图1,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点;(请在横线上填是或不是)
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所对应的点是【M,N】的好点(写出所有可能的情况);
拓展提升:
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过几秒时,P、A和B中恰有一个点为其余两点的好点?(写出所有情况)
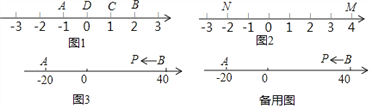
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用科学记数法表示下列各数:
(1)中国森林面积有128630000公顷,
(2)2008年临沂市总人口达l022.7万人,
(3)地球到太阳的距离大约是150000000千米,
(4)光年是天文学中的距离单位,1光年大约是950000000000千米,
(5)2008年北京奥运会门票预算收入为140000000美元,
(6)一只苍蝇腹内的细菌多达2 800万个,(在使用科学技术法时要注意单位的转换,如1万=104,1亿=108)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把30974四舍五入,使其精确到千位,那么所得的近似数是( )
A. 3.10×105 B. 3.10×104 C. 3.10×103 D. 3.09×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com