C
分析:首先设各同心圆的半径分别为:r,2r,3r,4r,5r,由圆的面积公式,即可求得10环,9环,8环,7环,6环各部分的面积,继而可求得射中10环,9环,8环,7环,6环各部分的概率,比较大小,即可求得答案.
解答:设各同心圆的半径分别为:r,2r,3r,4r,5r,
∴各同心圆的面积为:πr
2,4πr
2,9πr
2,16πr
2,25πr
2,
∴10环,9环,8环,7环,6环各部分的面积分别是:πr
2,4πr
2-πr
2=3πr
2,9πr
2-4πr
2=5πr
2,16πr
2-9πr
2=7πr
2,25πr
2-16πr
2=9πr
2,
∴射中10环,9环,8环,7环,6环各部分的概率分别是:
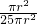
=

,
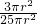
=
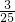
,
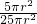
=
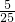
=

,
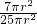
=

,
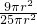
=

,
∴可能性最小的是射中第10环.
故选C.
点评:此题考查了几何概率的知识.注意掌握几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

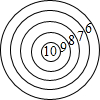 射击打靶训练时,靶子(如图)是由5个多轮的同心圆构成,那么可能性最小的是射中
射击打靶训练时,靶子(如图)是由5个多轮的同心圆构成,那么可能性最小的是射中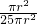 =
= ,
,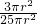 =
=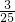 ,
,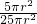 =
=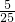 =
= ,
,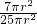 =
= ,
,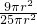 =
= ,
,
