
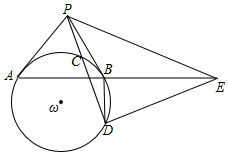
 如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB.
如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB. 分析 如图,连接Pω交AE于F,连接AC、DF、ωD、ωB、直线Cω交⊙ω于M,交PE于H.首先证明△PFD∽△PCω,推出∠PDF=∠PωC,由∠PFC=∠PDE=90°,推出P、F、D、E四点共圆,推出∠PEF=∠PDF=∠FωO,由∠FOω=∠HOE,推出∠OHE=∠OFω=90°,由∠GHP=∠GBω=90°,∠PGH=∠BGω,推出∠GPH=∠BωG,由∠BωG=2∠PDB,推出∠EPB=2∠PDB.
解答 证明:如图,连接Pω交AE于F,连接AC、DF、ωD、ωB、直线Cω交⊙ω于M,交PE于H.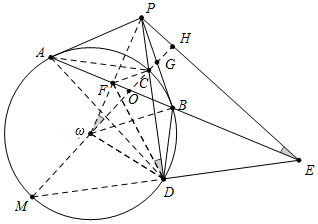
∵PA、PB是切线,
∴Pω⊥AB,ωB⊥PB,
∵∠BPF=∠BPω,∠PFB=∠PBω,
∴△PFB∽△PBω,
∴PB2=PF•Pω,
∵PB2=PC•PD(切割线定理,可以用相似三角形证明),
∴PF•Pω=PC•PD,
∴$\frac{PF}{PC}$=$\frac{PD}{Pω}$,∵∠FPD=∠ωPC,
∴△PFD∽△PCω,
∴∠PDF=∠PωC,
∵∠PFC=∠PDE=90°,
∴P、F、D、E四点共圆,
∴∠PEF=∠PDF=∠FωO,
∵∠FOω=∠HOE,
∴∠OHE=∠OFω=90°,
∵∠GHP=∠GBω=90°,∠PGH=∠BGω,
∴∠GPH=∠BωG,
∵∠BωG=2∠PDB,
∴∠EPB=2∠PDB.
点评 本题考查切线的性质、相似三角形的判定和性质、切线长定理、四点共圆、圆周角定理等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,本题比较难,属于竞赛题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
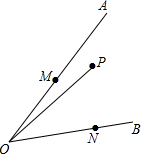 如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运运,若∠AOB=45°,OP=2$\sqrt{2}$,则△PMN的周长的最小值为4.
如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运运,若∠AOB=45°,OP=2$\sqrt{2}$,则△PMN的周长的最小值为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com