
 ,试求不等式(a-4b)x+2a-3b>0的解.
,试求不等式(a-4b)x+2a-3b>0的解. ,
,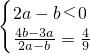 ,
, b;
b; b-b<0,即b<0;
b-b<0,即b<0; b-4b)x+
b-4b)x+ b-3b>0,即b(-
b-3b>0,即b(-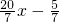 )>0,
)>0, x-
x- <0,
<0, .
. .
. ,可解得ab的关系式.再求根据ab的关系求不等式(a-4b)x+2a-3b>0的解即可.
,可解得ab的关系式.再求根据ab的关系求不等式(a-4b)x+2a-3b>0的解即可.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com