练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若2m-4与3m-1是同一个数的平方根，则m的值是（ ）

    A. -3B. 1C. -3或1D. 3

    【答案】C

    【解析】

    由于一个正数的平方根有两个，且互为相反数，可得到2m-4与3m-1互为相反数，2m-4与3m-1也可以是同一个数．

    解：∵2m-4与3m-1是同一个数的平方根，
    ∴2m-4+3m-1=0，或2m-4=3m-1，
    解得：m=1或-3．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB=120°，∠COD在∠AOB内部且∠COD=60°，下列说法：

    ①如果∠AOC=∠BOD，则图中有两对互补的角；

    ②如果作OE平分∠BOC，则∠AOC=2∠DOE；

    ③如果作OM平分∠AOC，且∠MON=90°，则ON平分∠BOD；

    ④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ，则，

    其中正确的有（ ）个.

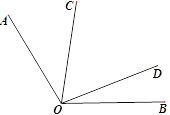
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，是真命题的是（ ）

    A. 两条直线被第三条直线所截，同位角相等B. 垂直于同一直线的两直线平行

    C. 相等的角是对顶角D. 平行于同一直线的两直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 中，点在边上， ⊥， ⊥，垂足分别是、，∠1＝∠2.

    （1）与平行吗？为什么？

    （2）若∠＝51°，∠＝54°，求∠的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近年来，各地“广场舞”噪音干扰的问题倍受关注．相关人员对本地区15~65岁年龄段的市民进行了随机调查，并制作了如下相应的统计图．市民对“广场舞”噪音干扰的态度有以下五种：A．没影响 B．影响不大 C．有影响，建议做无声运动 D．影响很大，建议取缔 E．不关心这个问题

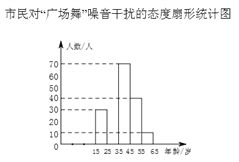
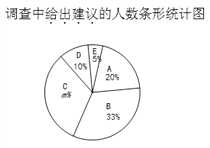
    根据以上信息解答下列问题：

    （1）根据统计图填空： ，A区域所对应的扇形圆心角为 度；

    (2)在此次调查中，“不关心这个问题”的有25人，请问一共调查了多少人？

    (3)将条形统计图补充完整；

    (4)若本地共有14万市民，依据此次调查结果估计本地市民中会有多少人给出建议？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程符合题意的是（ ）

    A.(x＋2)2＋(x－4)2＝x2B.(x－2)2＋(x－4)2＝x2

    C.x2＋(x－4)2＝(x－4)2D.(x－2)2＋x2＝(x＋4)2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【新知理解】

    如图①，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”.

    线段的中点__________这条线段的“巧点”；（填“是”或“不是”）.

    若AB = 12cm，点C是线段AB的巧点，则AC=___________cm；

    【解决问题】

    （3） 如图②，已知AB=12cm.动点P从点A出发，以2cm/s的速度沿AB向点B匀速移动：点Q从点B出发，以1cm/s的速度沿BA向点A匀速移动，点P、Q同时出发，当其中一点到达终点时，运动停止，设移动的时间为t（s）.当t为何值时，A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点？说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了深化课程改革，省实验积极开展校本课程建设，计划成立“增量阅读”、“趣味数学”、“音乐舞蹈”和“戏剧英语”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了初中部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：

    选择意向

    增量阅读

    趣味数学

    音乐舞蹈

    戏曲英语

    其他

    所占百分比

    a

    20%

    b

    10%

    5%


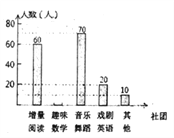
    根据统计图表的信息，解答下列问题：

    (l)求本次抽样调查的学生总人数及a、b的值：

    (2)将条形统计图补充完整；

    (3)若该校共有5000名学生，试估计全校选择“音乐舞蹈”社团的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按图填空，并注明理由．

    ⑴完成正确的证明：如图，已知AB∥CD，求证：∠BED=∠B+∠D

    证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）

    ∴∠1= （ ）

    ∵AB∥CD（已知）

    ∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）

    ∴∠2= （ ）

    又∠BED=∠1+∠2

    ∴∠BED=∠B+∠D （等量代换）．

    ⑵如图，在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．

    解：因为EF∥AD（已知）

    所以∠2=∠3．（ ）

    又因为∠1=∠2，所以∠1=∠3．（等量代换）

    所以AB∥ （ ）

    所以∠BAC+ =180°（ ）．

    又因为∠BAC=70°，所以∠AGD=110°．

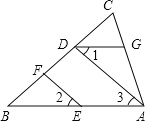
    图⑴ 图⑵

    查看答案和解析>>

    同步练习册答案