
分析 要求x的整数值可以进行分段计算,令x+3=0或x-2=0时,分为3段进行计算,最后确定x的值.
解答 解:令x+3=0或x-2=0时,则x=-3或x=2
当x<-3时,
∴-(x+3)-(x-2)=5,
-x-3-x+2=5,
x=-3(范围内不成立)
当-3≤x≤2时,
∴(x+3)-(x-2)=5,
x+3-x+2=5,
5=5,
∴x=-3,-2,-1,0,1,2,
当x>2时,
∴(x+,3)+(x-2)=5,
x+3+x-2=5,
2x=4,
x=2(范围内不成立)
综上所述,符合条件的整数x有:-3,-2,-1,0,1,2.
故答案为:-3,-2,-1,0,1,2.
点评 本题主要考查了去绝对值和数轴相联系的综合试题以及去绝对值的方法和去绝对值在数轴上的运用,难度较大,去绝对值的关键是确定绝对值里面的数的正负性.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
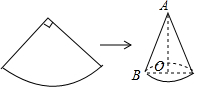 如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.
如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
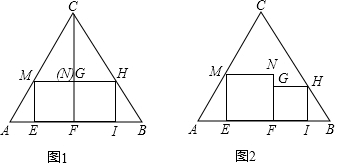
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
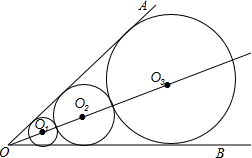 如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.
如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
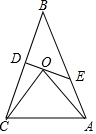 如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$.
如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com