
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
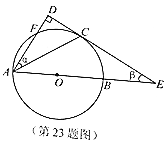
(1)用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() ,
,![]() 的值.
的值.
【答案】(1)β=90°-2α(0°<α<45°);(2)α=β=30°.
【解析】
试题分析:(1)首先证明∠DAE=2α,在Rt△ADE中,根据两锐角互余,可知2α+β=90°,(0°<α<45°);
(2)连接OF交AC于O′,连接CF.只要证明四边形AFCO是菱形,推出△AFO是等边三角形即可解决问题;
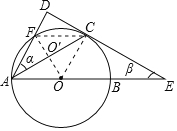
试题解析:(1)连接OC.
∵DE是⊙O的切线,∴OC⊥DE,
∵AD⊥DE,∴AD∥OC,∴∠DAC=∠ACO,
∵OA=OC,∴∠OCA=∠OAC,∴∠DAE=2α,
∵∠D=90°,∴∠DAE+∠E=90°,
∴2α+β=90°(0°<α<45°),即β=90°-2α(0°<α<45°).
(2)连接OF交AC于O′,连接CF.
∵AO′=CO′,∴AC⊥OF,∴FA=FC,∴∠FAC=∠FCA=∠CAO,
∴CF∥OA,∵AF∥OC,∴四边形AFCO是平行四边形,
∵OA=OC,∴四边形AFCO是菱形,∴AF=AO=OF,
∴△AOF是等边三角形,∴∠FAO=2α=60°,∴α=30°,
∵2α+β=90°,∴β=30°,∴α=β=30°.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE. 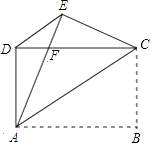
(1)求证:△DEC≌△EDA;
(2)求DF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.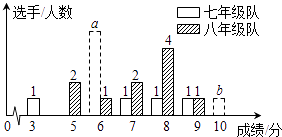
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中.适合采取全面调查方式的是( )
A.了解某城市的空气质量的情况B.了解全国中学生的视力情况
C.了解某企业对应聘人员进行面试的情况D.了解某池塘中鱼的数量的情况
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com