【题目】计算：（1）
；（2） 
（3）
；（4）
【答案】（1）3；（2）5a3；(3)8a3b3-4a2b2+12ab；(4) 2xy+2y2
【解析】试题分析：（1）第一项根据一个数的负整数指数幂等于这个数的正整数指数幂的倒数计算，第二项根据非零数的零次幂等于1计算；（2）先算除法，再算减法；（3）按照单项式乘多项式的乘法法则计算；（4）
根据完全平方公式计算， 
根据平方差公式计算，然后去括号合并同类项.
解：（1）
=4-1
=3；
（2）
= 
= 
；
（3）
=4ab×2a2b2-4ab×ab+4ab×3
=8a3b3-4a2b2+12ab；
（4）
=x2+2xy+y2-(x2-y2)
= x2+2xy+y2-x2+y2
=2xy+2y2.
科目：初中数学 来源： 题型：
【题目】若a+b＜0，a＜0，b＞0，则a，﹣a，b，﹣b的大小关系是（ ）
A. a＜﹣b＜b＜﹣a B. ﹣b＜a＜﹣a＜b C. a＜﹣b＜﹣a＜b D. ﹣b＜a＜b＜﹣a
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】画图并填空：如图，每个小正方形的边长为1个单位，每个小正方形的顶点叫格点.
（1）将△ABC向左平移8格，再向下平移1格．请在图中画出平移后的△A′B′C′
（2）利用网格在图中画出△ABC的中线CD，高线AE；
（3）△A′B′C′的面积为_____．
（4）在平移过程中线段BC所扫过的面积为 .
（5）在右图中能使
的格点P的个数有 个(点P异于A).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AD∥BC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E，试说明AB∥DC，把下面的说理过程补充完整．
证明：∵AD∥BC（已知）
∴∠2=∠E（___________________________）
∵AE平分∠BAD（已知）
∴∠1=∠2 （_________________________）
∴∠1=∠E（___________________________）
∵∠CFE=∠E（已知）
∴∠1=∠______（______________________）
∴AB∥CD（_________________________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移后得△DEF，使点A的对应点为点D，点B的对应点为点E．
（1）画出△DEF；
（2）连接AD、BE，则线段AD与BE的关系是 ；
（3）求△DEF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？
操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，记录球的颜色，放回盒中，然后重复上述过程。
活动结果：摸球实验活动一共做了50次，统计结果如下表：
推测计算：由上述的摸球实验可推算：
（1）盒中红球、黄球各占总球数的百分比分别是多少？
（2）盒中有红球多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
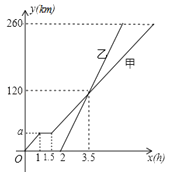
【题目】甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．
（1）求出图中a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数表达式，并写出相应的x的取值范围；
（3）当甲车行驶多长时间时，两车恰好相距40km．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下：
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)．
（1）这6名选手笔试成绩的中位数是________分，众数是________分；
（2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；
（3）求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com