
分析 (1)根据题意可以得到yA、yB与x之间的函数关系式;
(2)根据(1)中函数关系式,利用分类讨论的数学方法可以解答本题.
解答 解:(1)由题意可得,
yA=(20×60+20x×2)×0.9=36x+1080,
当2≤x≤4时,yB=20×60=1200,
当x>4时,yB=20×60+(x-4)×20×2=40x+1040,
即yA与x之间的函数关系式为yA=36x+1080,
yB与x之间的函数关系式为yB=$\left\{\begin{array}{l}{1200}&{(2≤x≤4)}\\{40x+1040}&{(x>4)}\end{array}\right.$;
(2)由题意可得,
当36x+1080<1200时,x<$\frac{10}{3}$,
∴当x为2或3时,从A商店购买,当x为4时,在B商店购买,
当36x+1080<40x+1040时,得x>10,
∴当4<x<10时,在B商店购买,
当x=10时,在哪家商店购买都可以,
当x>10时,在A商店购买,
由上可得,当x=2,x=3或x>10(x取整数)时,在A商店购买,
当x=10时,在哪家商店购买都可以,
当4≤x<10(x取整数)时,在B商店购买.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答,注意题目中x≥2.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
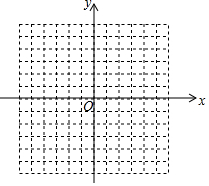 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
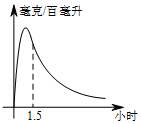 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
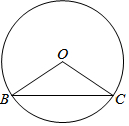 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com