【题目】如图，已知△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．
（1）求证：四边形ADCE是菱形；
（2）求证：BC=ED．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：
（1）由△ABC中，∠ACB=90°，CE是中线，可证得：CE=AE，再由△ACD与△ACE关于直线AC对称，可得：AD=AE=CE=CD，从而可得四边形ADCE是菱形；
（2）由（1）可得DC∥BE，DC=AE=BE，从而可证得：四边形BCDE是平行四边形，就可得到：BC=DE.
试题解析：
（1）证明：∵∠C=90°，点E为AB的中点，
∴EA=EC，
∵△ACD与△ACE关于直线AC对称．
∴△ACD≌△ACE，
∴EA=EC=DA=DC，
∴四边形ADCE是菱形；
（2）∵四边形ADCE是菱形，
∴CD∥AE且CD=AE，
∵AE=EB，
∴CD∥EB且CD=EB
∴四边形BCDE为平行四边形，
∴DE=BC．
金钥匙试卷系列答案科目：初中数学 来源： 题型：
【题目】将抛物线y=x2向左平移2个单位，再向下平移5个单位，平移后所得新抛物线的表达式为（ ）
A. y=（x+2）2﹣5 B. y=（x+2）2+5 C. y=（x﹣2）2﹣5 D. y=（x﹣2）2+5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习“二元一次方程组的解”时，数学张老师设计了一个数学活动，有A、B两组卡片，每组各三张，A组卡片上分别写有0,1,2；B组卡片上分别写有-3，-1,1。每张卡片除正面写有不同数字外，其余均相同。甲从A组随机抽取一张记为x，乙从B组随机抽取一张记为y。
(1)若甲抽出的数字是2，乙抽出的数字是-1，它们恰好是方程ax-y=5的解，求a的值；
(2)求甲、乙随机抽取一次的数恰好是方程ax-y=3的解得概率（请用树状图或列表法求解
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：
由于a≠0，方程ax2+bx+c=0变形为：
x2+
x=﹣
，…第一步
x2+
x+（
）2=﹣
+（
）2，…第二步
（x+
）2=
，…第三步
x+
=
（b2﹣4ac＞0），…第四步
x=
，…第五步
嘉淇的解法从第 步开始出现错误；事实上，当b2﹣4ac＞0时，方程ax2+bx+c=0（a≠O）的求根公式是 ．
用配方法解方程：x2﹣2x﹣24=0．
查看答案和解析>>
科目：初中数学 来源： 题型：
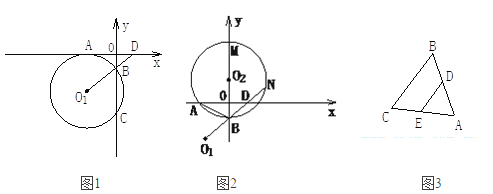
【题目】如图1，平面直角坐标系中，⊙O1与x轴相切于点A（-2，0），与y轴交于B、C两点，O1B的延长线交x轴于点D（
，0），连结AB．
（1）求证：∠ABO1=∠ABO；
（2）设E为优弧
的中点，连结AC、BE交于点F，请你探求BE·BF的值．
（3）如图2，过A、B两点作⊙O2与y轴的正半轴交于点M，与BD的延长线交于点N，当⊙O2的大小变化时，给出下列两个结论．
①BM-BN的值不变；②BM+BN的值不变，其中有且只有一个结论是正确的，请你判断哪一个结论正确，证明正确的结论并求出其值．
（友情提示：如图3，如果DE∥BC，那么
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用反证法证明命题“三角形的内角中至少有一个不大于60°”时，假设正确的是
A. 假设三内角都大于60°B. 假设三内角都不大于60°
C. 假设三内角至多有一个大于60°D. 假设三内角至多有两个大于60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com