
 如图,∠1=m°,∠2+∠4+∠6+∠8=n°,则∠3+∠5+∠7的大小是m°+n°.
如图,∠1=m°,∠2+∠4+∠6+∠8=n°,则∠3+∠5+∠7的大小是m°+n°. 分析 连结AB、BC、CD,形成一个五边形和三个三角形.由三个三角形内角和和为540°得出(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,得出∠3+∠5+∠7=540°-(∠9+∠10+∠11+∠12+∠13+∠14),由五边形ABCDE的内角和为540°,得出∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8=540°,即可求得∠9+∠10+∠11+∠12+∠13+∠14=540°-(m°+n°).将∠9+∠10+∠11+∠12+∠13+∠14=540°-(m°+n°)代入,即可得出∠3+∠5+∠7=m°+n°.
解答 解:如图,连结AB、BC、CD.
∵(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,
∴(∠3+∠5+∠7)+(∠9+∠10+∠11+∠12+∠13+∠14)=540°,
∴∠3+∠5+∠7=540°-(∠9+∠10+∠11+∠12+∠13+∠14),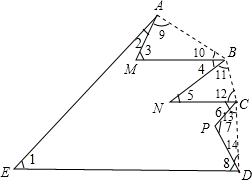 ∵五边形ABCDE的内角和为(5-2)×180°=540°,
∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴540°=∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8
=(∠1+∠2+∠4+∠6+∠8)+(∠9+∠10+∠11+∠12+∠13+∠14)
=(m°+n°)+(∠9+∠10+∠11+∠12+∠13+∠14),
∴∠9+∠10+∠11+∠12+∠13+∠14=540°-(m°+n°).
∴∠3+∠5+∠7=540°-[540°-(m°+n°)]=m°+n°.
故答案为m°+n°.
点评 本题考查了多边形内角和定理,难度适中.准确作出辅助线利用数形结合是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
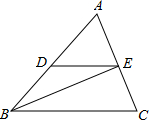 如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
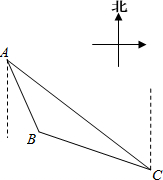 如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计),观测得点在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米,问:
如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计),观测得点在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com