
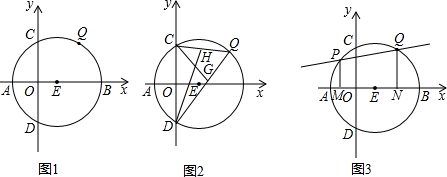
分析 (1)如图1中,连接EQ,作QH⊥OB于H,在Rt△EQH中,利用勾股定理即可解决问题.
(2)CH+DG的值是定值.如图2中,在CD上截取一点K,使得CK=CH,CG与DH交于点M,连接EC、ED.只要证明△CMH≌△CMK,△DMG≌△DMK,推出DK=DG,得到CH+DG=CK+CK=CD=2CO,即可解决问题.
(3)如图3中,圆心坐标为(2,0),半径为4,可知圆上的点(x,y)满足(x-2)2+y2=16,由$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{(x-2)^{2}+{y}^{2}=16}\end{array}\right.$得到$\frac{5}{4}$x2+(b-4)x+b2-12=0,设两根为x1,x2,
可得x1+x2=$\frac{4}{5}$(4-b),x1x2=$\frac{4}{5}$(b2-12),因为|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{16}{25}(4-b)^{2}-\frac{16}{5}({b}^{2}-12)}$=$\sqrt{-\frac{64}{25}{b}^{2}-\frac{128}{25}b+\frac{1216}{25}}$,所以PM+NQ=y1+y1=$\frac{1}{2}({x}_{1}+{x}_{2})$+2b=$\frac{8}{5}$(b+1),由PQ=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{1+\frac{1}{4}}$•$\sqrt{\frac{16}{25}(4-b)^{2}-\frac{16}{5}({b}^{2}-12)}$=$\sqrt{-\frac{16}{5}{b}^{2}-\frac{32}{5}b+\frac{304}{5}}$,根据PM+QN=PQ,列出方程即可解决问题.
解答 解:(1)如图1中,连接EQ,作QH⊥OB于H.
∵OA=OE=2,Q(2+2$\sqrt{3}$,n),
∴OH=2+2$\sqrt{3}$,EQ=EA=4,
在Rt△EQH中,∠EHQ=90°,EQ=4,EH=OH-OE=2$\sqrt{3}$,
∴QH=$\sqrt{E{Q}^{2}-E{H}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴n=2.
(2)CH+DG的值是定值.
理由:如图2中,在CD上截取一点K,使得CK=CH,CG与DH交于点M,连接EC、ED.
∵CG、DH分别平分∠QCD、∠QDC,
∴∠GCD=$\frac{1}{2}$QCD,∠HDC=$\frac{1}{2}$∠QDC,
∵在Rt△EOC中,∵EC=2EO,
∴∠ECO=30°,
∴∠CEO=60°,同理∠DEO=60°,
∴∠CED=120°,∠Q=$\frac{1}{2}$∠CED=60°,
∴∠MCD+∠MDC=$\frac{1}{2}$(180°-∠Q)=60°,
∴∠CMD=180°-(∠MCD+∠MDC)=120°,
∴∠CMH=∠DMG=60°,
在△CMH和△CMK中,
$\left\{\begin{array}{l}{CM=CM}\\{∠MCH=∠MCK}\\{CH=CK}\end{array}\right.$,
∴△CMH≌△CMK,
∴∠CMH=∠CMK=60°,
∴∠DMK=∠DMG,
在△DMG和△DMK中,
$\left\{\begin{array}{l}{∠DMG=∠DMK}\\{DM=DM}\\{∠MDG=∠MDK}\end{array}\right.$,
∴△DMG≌△DMK,
∴DK=DG,
∴CH+DG=CK+CK=CD=2CO=4$\sqrt{3}$.
(3)如图3中,∵圆心坐标为(2,0),半径为4,
∴圆上的点(x,y)满足(x-2)2+y2=16,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{(x-2)^{2}+{y}^{2}=16}\end{array}\right.$消去y得到$\frac{5}{4}$x2+(b-4)x+b2-12=0,设两根为x1,x2,
∴x1+x2=$\frac{4}{5}$(4-b),x1x2=$\frac{4}{5}$(b2-12),
∵|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{16}{25}(4-b)^{2}-\frac{16}{5}({b}^{2}-12)}$=$\sqrt{-\frac{64}{25}{b}^{2}-\frac{128}{25}b+\frac{1216}{25}}$,
∴PM+NQ=y1+y1=$\frac{1}{2}({x}_{1}+{x}_{2})$+2b=$\frac{8}{5}$(b+1),
∵PQ=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{1+\frac{1}{4}}$•$\sqrt{\frac{16}{25}(4-b)^{2}-\frac{16}{5}({b}^{2}-12)}$=
$\sqrt{-\frac{16}{5}{b}^{2}-\frac{32}{5}b+\frac{304}{5}}$,
∵PM+QN=PQ,
∴$\frac{8}{5}$(b+1)=$\sqrt{-\frac{16}{5}{b}^{2}-\frac{32}{5}b+\frac{304}{5}}$,
整理得9b2+18b-91=0,
∴(3b+13)(3b-7)=0,
∴b=$\frac{7}{3}$或-$\frac{13}{3}$(舍弃),
∴b=$\frac{7}{3}$.
点评 本题考查圆综合题、全等三角形的判定和性质、勾股定理、一元二次方程的根与系数关系,一次函数等知识,解题的关键是灵活运用所学知识解决问题,题目比较难,有一定的技巧性,学会把问题转化为一元二次方程,利用根与系数关系解决问题,所以中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把下列各数在数轴上表示出来,并用“<”把它们连接起来.
把下列各数在数轴上表示出来,并用“<”把它们连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.
如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
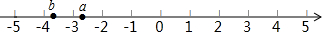 我们知道:a、b在数轴上对应的A、B两点之间距离|AB|=|a-b|
我们知道:a、b在数轴上对应的A、B两点之间距离|AB|=|a-b|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
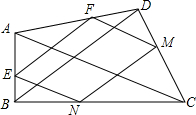 如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.
如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com