解:(1)令y=3x+3=0得:x=-1,
故点C的坐标为(-1,0);
令x=0得:y=3x+3=3×0+3=3
故点A的坐标为(0,3);
∵△OAB是等腰直角三角形.
∴OB=OA=3,
∴点B的坐标为(3,0),
设过A、B、C三点的抛物线的解析式y=ax
2+bx+c,

解得:
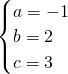
∴解析式为:y=-x
2+2x+3;
(2)设直线AB的解析式为y=kx+b,
∴

解得:
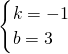
∴直线AB的解析式为:y=-x+3
∵线CD∥AB
∴设直线CD的解析式为y=-x+b
∵经过点C(-1,0),
∴-(-1)+b=0
解得:b=-1,
∴直线CD的解析式为:y=-x-1,
令-x-1=-x
2+2x+3,
解得:x=-1,或x=4,
将x=4代入y=-x
2+2x+3=-16+2×4+3=-5,
∴点D的坐标为:(4,-5);
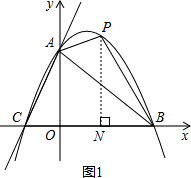
(3)存在.如图1所示,设P(x,y)是第一象限的抛物线上一点,
过点P作PN⊥x轴于点N,则ON=x,PN=y,BN=OB-ON=3-x.
S
△ABP=S
梯形PNOA+S
△PNB-S
△AOB=

(OA+PN)•ON+

PN•BN-

OA•OB
=

(3+y)•x+

y•(3-x)-

×3×3
=

(x+y)-

,
∵P(x,y)在抛物线上,∴y=-x
2+2x+3,代入上式得:
S
△ABP=

(x+y)-

=-

(x
2-3x)=-

(x-

)
2+
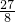
,
∴当x=

时,S
△ABP取得最大值.
当x=

时,y=-x
2+2x+3=

,
∴P(

,

).
所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;
P点的坐标为(

,

).
分析:(1)求得直线y=3x+3与坐标轴的两交点坐标,然后根据OB=OA即可求得点B的坐标,然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可;
(2)首先利用待定系数法求得直线AB的解析式,然后根据CD∥AB得到两直线的k值相等,根据直线CD经过点C求得直线CD的解析式,然后求得直线CD和抛物线的交点坐标即可;
(3)本问关键是求出△ABP的面积表达式.这个表达式是一个关于P点横坐标的二次函数,利用二次函数求极值的方法可以确定P点的坐标.
点评:本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式、图形面积的表示方法等重要知识点,难度不是很大.注意第(3)问中图形面积的表示方法-并非直接用底乘以高,而是通过其他图形组合转化而来-这是压轴题中常见的技巧,需要认真掌握.

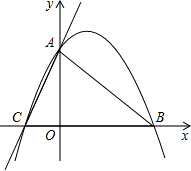 已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
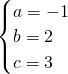

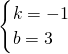

 (OA+PN)•ON+
(OA+PN)•ON+ PN•BN-
PN•BN- OA•OB
OA•OB (3+y)•x+
(3+y)•x+ y•(3-x)-
y•(3-x)- ×3×3
×3×3 (x+y)-
(x+y)- ,
, (x+y)-
(x+y)- =-
=- (x2-3x)=-
(x2-3x)=- (x-
(x- )2+
)2+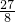 ,
, 时,S△ABP取得最大值.
时,S△ABP取得最大值. 时,y=-x2+2x+3=
时,y=-x2+2x+3= ,
, ,
, ).
). ,
, ).
).

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=