(1)解:∵一次函数y=x+m-2与二次函数y=x
2-2的图象有两个交点,
∴关于x的方程x+m-2=x
2-2有两个不相等的实数根,即△>0,
方程变形为x
2-x-m=0,△=1+4m>0,解得m>-

,
即m的取值范围为m>-

;
(2)证明:设点A、B的横坐标分别为x
1,x
2,则为x
1-x
2=3,
∴(x
1-x
2)
2=9,
∴(x
1+x
2)
2-4x
1x
2=9,
对于x
2-x-m=0,x
1+x
2=1,x
1•x
2=-m,
∴1+4m=9,解得m=2,
∴x
2-x-2=0,解此方程得x
1=2,x
2=-1,
当x=2,则y=4-2=2;当x=-1,则y=1-2=-1,
∴A点坐标为(2,2),B点坐标为(-1,-1),如图,C点坐标为(0,-2),
BC=

,AB=3

,AC=2

,
∴BC
2+AB
2=AC
2,
∴△ABC为直角三角形;
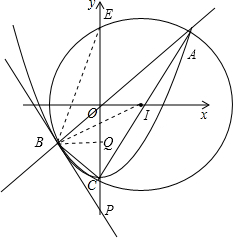
(3)解:∵AC为Rt△ABC的斜边,并且AC与x轴的交点(1,0)为AC的中点,
∴△ABC的外接圆⊙I的圆心I的坐标为(1,0),
⊙I与y轴的另一个交点为E,则点E与C关于x轴对称,所以E点坐标为(0,2),
连IB,EB,过B点作IB的垂线交y轴于P点,BQ⊥y轴于Q,
∵∠ABC=90°,∠IBP=90°,
∴∠ABI=∠PBC,
而∠ABI=∠BAI=∠BEC,
∴∠PBC=∠BEC,
∴△PBC∽△PEB,
∴PB:PE=PC:PB,即PB
2=PE•PC,
设P(0,y),则EP=2-y,CP=-2-y,QP=-1-y,
∴1+(-1-y)
2=(2-y)(-2-y),
解得y=-3,
∴P点坐标为(0,-3),
设直线PB的解析式为y=kx+b,把B(-1,-1)、P(0,-3)代入得,-k+b=-1,b=-3,
解得k=-2,b=-3,
∴过点B的⊙I的切线的解析式为y=-2x-3.
分析:(1)根据题意得到关于x的方程x+m-2=x
2-2有两个不相等的实数根,即△>0,即,△=1+4m>0,解不等式即可确定m的取值范围;
(2)设点A、B的横坐标分别为x
1,x
2,则为x
1-x
2=3,则(x
1-x
2)
2=9,根据一元二次方程的根与系数的关系有x
1+x
2=1,x
1•x
2=-m,得到1+4m=9,解得m=2,
解方程x
2-x-2=0得x
1=2,x
2=-1,则A点坐标为(2,2),B点坐标为(-1,-1),且C点坐标为(0,-2),利用勾股定理可计算出BC=

,AB=3

,AC=2

,
则有BC
2+AB
2=AC
2,即可得到结论;
(3)AC为Rt△ABC的斜边,并且AC与x轴的交点(1,0)为AC的中点,则△ABC的外接圆⊙I的圆心I的坐标为(1,0),⊙I与y轴的另一个交点为E,由垂径定理可得点E与C关于x轴对称,所以E点坐标为(0,2),连IB,EB,过B点作IB的垂线交y轴于P点,BQ⊥y轴于Q;利用等角的余角线段得∠ABI=∠PBC,根据圆周角定理易得
∠ABI=∠BAI=∠BEC,则∠PBC=∠BEC,于是△PBC∽△PEB,得PB:PE=PC:PB,即PB
2=PE•PC,设P(0,y),则EP=2-y,CP=-2-y,QP=-1-y,1+(-1-y)
2=(2-y)(-2-y),解得y=-3,得到P点坐标为(0,-3),然后利用待定系数法确定直线BP的解析式.
点评:本题考查了二次函数的综合题:运用一元二次方程的根的判别式和根与系数的关系确定直线与二次函数图形的交点坐标,由坐标有关计算线段的长来判断几何图形的性质;同时运用了直角三角形的性质和圆的切线性质以及三角形相似的判定与性质.

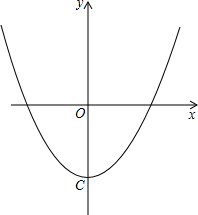 已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.
已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.
 ,
, ;
; ,AB=3
,AB=3 ,AC=2
,AC=2 ,
, ,AB=3
,AB=3 ,AC=2
,AC=2 ,
,
