Question

有一块直角三角形木板如图所示，已知∠C=90°，AB=5cm，BC=3cm，根据需要，要把它加工成一个面积最大的正方形木板，设计一个方案，应怎样裁，才能使正方形木板面积最大？并求出这个正方形木板的边长．

Answer 1

分析：方案一：根据题意画出图形，作CM⊥AB于M，交DE于N．设正方形边长为xcm，再根据直角三角形的面积得出CM的长，利用相似三角形的判定定理即可得出△CDE∽△CAB，再根据相似三角形的对应边成比例即可求出正方形的边长；
方案二：如图（2）设正方形边长为ycm，利用相似三角形的判定定理即可得出△BFE∽△BCA，再根据相似三角形的对应边成比例即可求出正方形的边长；把两方案中正方形的边长进行比较即可得出结论．

解答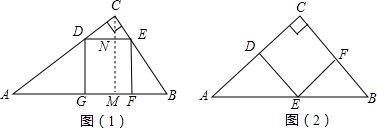：解：方案一：如图（1），
作CM⊥AB于M，交DE于N．
设正方形边长为xcm．
由S_△ABC=

1

2

AC•BC=

1

2

AB•CM
知：CM=

AC•BC

AB

=

12

5

（1分）
∵DE∥AB
∴△CDE∽△CAB，（2分）
即：

CN

CM

=

DE

AB

∴

12 5 -x

12 5

=

x

5

∴x=

60

37

（3分）
方案二：如图（2）设正方形边长为ycm．
∵EF∥AC
∴△BFE∽△BCA，（4分）
∴

BF

BC

=

EF

AC

即　

3-y

3

=

y

4

∴y=

12

7

=

60

35

（5分）
∵x＜y，
∴方案二裁出的正方形的面积最大．（6分）
这时正方形的边长是

12

7

cm．（7分）

点评：本题考查的是相似三角形在实际生活中的应用，能根据题意画出图形，作出辅助线，再根据相似三角形的判定定理及性质进行解答即可．