
如图,AB是⊙O的直径,C是⊙O上的一点,过点A作AD⊥CD于点D,交⊙O于点E,且 =
= .
.
(1)求证:CD是⊙O的切线;
(2)若tan∠CAB= ,BC=3,求DE的长.
,BC=3,求DE的长.

(1)证明见解析;(2)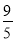 .
.
【解析】
试题分析:(1)连结OC,由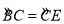 ,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BE交OC于F,由AB是⊙O的直径得∠ACB=90°,在Rt△ACB中,根据正切的定义得AC=4,再利用勾股定理计算出AB=5,然后证明Rt△ABC∽Rt△ACD,利用相似比先计算出AD=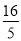 ,再计算出CD=
,再计算出CD=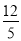 ;根据垂径定理的推论由
;根据垂径定理的推论由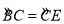 得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=
得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=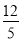 ,则BE=2EF=
,则BE=2EF=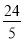 ,然后在Rt△ABE中,利用勾股定理计算出AE=,再利用DE=AD﹣AE求解.
,然后在Rt△ABE中,利用勾股定理计算出AE=,再利用DE=AD﹣AE求解.
试题解析:(1)证明:连结OC,如图,
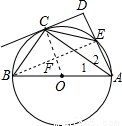
∵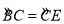 ,
,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠OCA,
∴∠2=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)【解析】
连结BE交OC于F,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,tan∠CAB=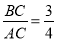 ,
,
而BC=3,
∴AC=4,
∴AB=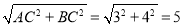 ,
,
∵∠1=∠2,
∴Rt△ABC∽Rt△ACD,
∴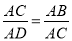 ,即
,即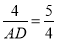 ,解得
,解得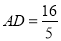 ,
,
∵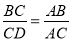 ,即
,即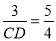 ,解得
,解得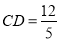 ,
,
∵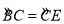 ,
,
∴OC⊥BE,BF=EF,
∴四边形DEFC为矩形,
∴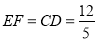 ,
,
∴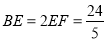 ,
,
∵AB为直径,
∴∠BEA=90°,
在Rt△ABE中, 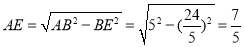 ,
,
∴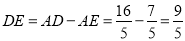 .
.
【考点】切线的判定.


科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:解答题
如图,二次函数y=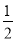 x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=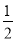 S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
如图是一个运算程序的示意图,若开始输入x的值为81,则第2014次输出的结果为( )

A.3 B.27 C.9 D.1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
如图是由几个小立方体快所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的小数,这个几何体的主视图是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com