
ИзНјЈ¬¶юҙОәҜКэy=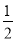 x2+bx+cөДНјПуҪ»xЦбУЪAЎўDБҪөгЈ¬Іўҫӯ№эBөгЈ¬ТСЦӘAөгЧшұкКЗЈЁ2Ј¬0Ј©Ј¬BөгөДЧшұкКЗЈЁ8Ј¬6Ј©Ј®
x2+bx+cөДНјПуҪ»xЦбУЪAЎўDБҪөгЈ¬Іўҫӯ№эBөгЈ¬ТСЦӘAөгЧшұкКЗЈЁ2Ј¬0Ј©Ј¬BөгөДЧшұкКЗЈЁ8Ј¬6Ј©Ј®
ЈЁ1Ј©Зу¶юҙОәҜКэөДҪвОцКҪЈ®
ЈЁ2Ј©ЗуәҜКэНјПуөД¶ҘөгЧшұкј°DөгөДЧшұкЈ®
ЈЁ3Ј©ёГ¶юҙОәҜКэөД¶ФіЖЦбҪ»xЦбУЪCөгЈ®Б¬ҪУBCЈ¬ІўСУіӨBCҪ»ЕЧОпПЯУЪEөгЈ¬Б¬ҪУBDЈ¬DEЈ¬ЗуЎчBDEөДГж»эЈ®
ЈЁ4Ј©ЕЧОпПЯЙПУРТ»ёц¶ҜөгPЈ¬УлAЈ¬DБҪөг№№іЙЎчADPЈ¬КЗ·сҙжФЪSЎчADP=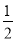 SЎчBCDЈҝИфҙжФЪЈ¬ЗлЗуіцPөгөДЧшұкЈ»ИфІ»ҙжФЪЈ®ЗлЛөГчАнУЙЈ®
SЎчBCDЈҝИфҙжФЪЈ¬ЗлЗуіцPөгөДЧшұкЈ»ИфІ»ҙжФЪЈ®ЗлЛөГчАнУЙЈ®

ЈЁ1Ј©¶юҙОәҜКэҪвОцКҪОӘЈәy=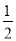 x2©Ғ4x+6Ј»
x2©Ғ4x+6Ј»
ЈЁ2Ј©әҜКэНјПуөД¶ҘөгЧшұкОӘЈЁ4Ј¬©Ғ2Ј©Ј¬өгDөДЧшұкОӘЈЁ6Ј¬0Ј©Ј»
ЈЁ3Ј©ЎчBDEөДГж»эОӘ7.5Ј®
ЈЁ4Ј©ҙжФЪЈ¬P1ЈЁ4+ Ј¬
Ј¬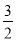 Ј©Ј¬P2ЈЁ4©Ғ
Ј©Ј¬P2ЈЁ4©Ғ Ј¬
Ј¬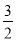 Ј©Ј¬P3ЈЁ3Ј¬©Ғ
Ј©Ј¬P3ЈЁ3Ј¬©Ғ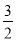 Ј©Ј¬P4ЈЁ5Ј¬©Ғ
Ј©Ј¬P4ЈЁ5Ј¬©Ғ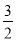 Ј©Ј®
Ј©Ј®
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©АыУГҙэ¶ЁПөКэ·ЁЗуіцbЈ¬cјҙҝЙЗуіц¶юҙОәҜКэҪвОцКҪЈ»
ЈЁ2Ј©°С¶юҙОәҜКэКҪЧӘ»ҜҝЙЦұҪУЗуіц¶ҘөгЧшұкЈ¬УЙA¶ФіЖ№ШПөҝЙЗуіцөгDөДЧшұкЈ»
ЈЁ3Ј©УЙҙэ¶ЁПөКэ·ЁҝЙЗуіцBCЛщФЪөДЦұПЯҪвОцКҪЈ¬УлЕЧОпПЯЧйіЙ·ҪіМЗуіцөгEөДЧшұкЈ¬АыУГЎчBDEөДГж»э=ЎчCDBөДГж»э+ЎчCDEөДГж»эЗуіцЎчBDEөДГж»эЈ»
ЈЁ4Ј©ЙиөгPөҪxЦбөДҫаАлОӘhЈ¬УЙSЎчADP=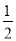 SЎчBCDЗуіцhөДЦөЈ¬ёщҫЭhөДХэЈ¬ёәЦөЗуіцөгPөДәбЧшұкјҙҝЙЗуіцөгPөДЧшұкЈ®
SЎчBCDЗуіцhөДЦөЈ¬ёщҫЭhөДХэЈ¬ёәЦөЗуіцөгPөДәбЧшұкјҙҝЙЗуіцөгPөДЧшұкЈ®
КФМвҪвОцЈәЈЁ1Ј©ЎЯ¶юҙОәҜКэy=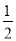 x2+bx+cөДНјПу№эAЈЁ2Ј¬0Ј©Ј¬BЈЁ8Ј¬6Ј©
x2+bx+cөДНјПу№эAЈЁ2Ј¬0Ј©Ј¬BЈЁ8Ј¬6Ј©
Ўа Ј¬ҪвөГ
Ј¬ҪвөГ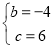
Ўа¶юҙОәҜКэҪвОцКҪОӘЈәy=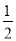 x2©Ғ4x+6Ј»
x2©Ғ4x+6Ј»
ЈЁ2Ј©УЙy=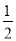 x2©Ғ4x+6Ј¬өГy=
x2©Ғ4x+6Ј¬өГy=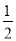 ЈЁx©Ғ4Ј©2©Ғ2Ј¬
ЈЁx©Ғ4Ј©2©Ғ2Ј¬
ЎаәҜКэНјПуөД¶ҘөгЧшұкОӘЈЁ4Ј¬©Ғ2Ј©Ј¬
ЎЯөгAЈ¬DКЗy=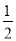 x2+bx+cУлxЦбөДБҪёцҪ»өгЈ¬
x2+bx+cУлxЦбөДБҪёцҪ»өгЈ¬
УЦЎЯөгAЈЁ2Ј¬0Ј©Ј¬¶ФіЖЦбОӘx=4Ј¬
ЎаөгDөДЧшұкОӘЈЁ6Ј¬0Ј©Ј»
ЈЁ3Ј©ЎЯ¶юҙОәҜКэөД¶ФіЖЦбҪ»xЦбУЪCөгЈ®
ЎаCөгөДЧшұкОӘЈЁ4Ј¬0Ј©
ЎЯBЈЁ8Ј¬6Ј©Ј¬
ЙиBCЛщФЪөДЦұПЯҪвОцКҪОӘy=kx+bЈ¬
Ўа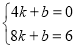 ҪвөГ
ҪвөГ
ЎаBCЛщФЪөДЦұПЯҪвОцКҪОӘy=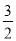 x©Ғ6Ј¬
x©Ғ6Ј¬
ЎЯEөгКЗy=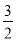 x©Ғ6Улy=
x©Ғ6Улy=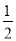 x2©Ғ4x+6өДҪ»өгЈ¬
x2©Ғ4x+6өДҪ»өгЈ¬
Ўа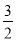 x©Ғ6=
x©Ғ6=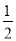 x2©Ғ4x+6
x2©Ғ4x+6
ҪвөГx1=3Ј¬x2=8ЈЁЙбИҘЈ©Ј¬
өұx=3КұЈ¬y=©Ғ3Ј¬
ЎаEЈЁ3Ј¬©Ғ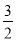 Ј©Ј¬
Ј©Ј¬
ЎаЎчBDEөДГж»э=ЎчCDBөДГж»э+ЎчCDEөДГж»э=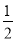 ЎБ2ЎБ6+
ЎБ2ЎБ6+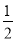 ЎБ2ЎБ
ЎБ2ЎБ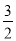 =7.5Ј®
=7.5Ј®
ЈЁ4Ј©ҙжФЪЈ¬
ЙиөгPөҪxЦбөДҫаАлОӘhЈ¬
ЎЯSЎчBCD=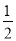 ЎБ2ЎБ6=6Ј¬SЎчADP=
ЎБ2ЎБ6=6Ј¬SЎчADP=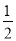 ЎБ4ЎБh=2hЈ¬
ЎБ4ЎБh=2hЈ¬
ЎЯSЎчADP=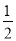 SЎчBCD
SЎчBCD
Ўа2h=6ЎБ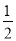 Ј¬ҪвөГh=
Ј¬ҪвөГh=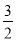 Ј¬
Ј¬
өұPФЪxЦбЙП·ҪКұЈ¬
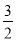 =
=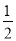 x2©Ғ4x+6Ј¬ҪвөГx1=4+
x2©Ғ4x+6Ј¬ҪвөГx1=4+ Ј¬x2=4©Ғ
Ј¬x2=4©Ғ Ј¬
Ј¬
өұөұPФЪxЦбПВ·ҪКұЈ¬
©Ғ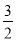 =
=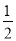 x2©Ғ4x+6Ј¬ҪвөГx1=3Ј¬x2=5Ј¬
x2©Ғ4x+6Ј¬ҪвөГx1=3Ј¬x2=5Ј¬
ЎаP1ЈЁ4+ Ј¬
Ј¬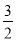 Ј©Ј¬P2ЈЁ4©Ғ
Ј©Ј¬P2ЈЁ4©Ғ Ј¬
Ј¬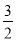 Ј©Ј¬P3ЈЁ3Ј¬©Ғ
Ј©Ј¬P3ЈЁ3Ј¬©Ғ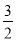 Ј©Ј¬P4ЈЁ5Ј¬©Ғ
Ј©Ј¬P4ЈЁ5Ј¬©Ғ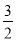 Ј©Ј®
Ј©Ј®
ҝјөгЈә¶юҙОәҜКэЧЫәПМвЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁБЙДюё§ЛіҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
ИзНјЈ¬ТСЦӘCO1КЗЎчABCөДЦРПЯЈ¬№эөгO1ЧчO1E1ЎОACҪ»BCУЪөгE1Ј¬Б¬ҪУAE1Ҫ»CO1УЪөгO2Ј»№эөгO2ЧчO2E2ЎОACҪ»BCУЪөгE2Ј¬Б¬ҪУAE2Ҫ»CO1УЪөгO3Ј»№эөгO3ЧчO3E3ЎОACҪ»BCУЪөгE3Ј¬ЎӯЈ¬ИзҙЛјМРшЈ¬ҝЙТФТАҙОөГөҪөгO4Ј¬O5Ј¬ЎӯЈ¬OnәНөгE4Ј¬E5Ј¬ЎӯЈ¬EnЈ®ФтOnEn=ЎЎЎЎACЈ®ЈЁУГә¬nөДҙъКэКҪұнКҫЈ©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁ№уЦЭЗӯОчҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ФЪТ»ёцІ»НёГчөДәРЧУЦРЧ°УР12ёц°ЧЗтЈ¬ИфёЙёц»ЖЗтЈ¬ЛьГЗіэСХЙ«І»Н¬НвЈ¬ЖдУаҫщПаН¬Ј®ИфҙУЦРЛж»ъГюіцТ»ёцЗтКЗ°ЧЗтөДёЕВККЗ Ј¬Фт»ЖЗтөДёцКэОӘЈЁ Ј©
Ј¬Фт»ЖЗтөДёцКэОӘЈЁ Ј©
AЈ®18 BЈ®20 CЈ®24 DЈ®28
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁ№уЦЭ№уСфҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
Ў°Бщ•Т»ЎұЖЪјдЈ¬РЎҪаөДВиВиҫӯУӘөДНжҫЯөкҪшБЛТ»ЦҪПдіэСХЙ«Нв¶јПаН¬өДЙўЧ°ЛЬБПЗт№І1000ёцЈ¬РЎҪаҪ«ЦҪПдАпГжөДЗтҪБФИәуЈ¬ҙУЦРЛж»ъГюіцТ»ёцЗтјЗПВЖдСХЙ«Ј¬°СЛь·Е»ШЦҪПдЦРЈ»ҪБФИәуФЩЛж»ъГюіцТ»ёцЗтјЗПВЖдСХЙ«Ј¬°СЛь·Е»ШЦҪПдЦРЈ»Ўӯ¶аҙОЦШёҙЙПКц№эіМәуЈ¬·ўПЦГюөҪәмЗтөДЖөВКЦрҪҘОИ¶ЁФЪ0Ј®2Ј¬УЙҙЛҝЙТФ№АјЖЦҪПдДЪәмЗтөДёцКэФјКЗ ёцЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁ№уЦЭ№уСфҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ФЪ°ај¶ЧйЦҜөДЎ°№уСфКРҙҙҪЁ№ъјТ»·ұЈДЈ·¶іЗКРЎұЦӘК¶ҫәИьЦРЈ¬РЎФГЛщФЪРЎЧй8ГыН¬С§өДіЙјЁ·ЦұрОӘЈЁөҘО»Јә·ЦЈ©95Ј¬94Ј¬94Ј¬98Ј¬94Ј¬90Ј¬94Ј¬90Ј¬ФтХв8ГыН¬С§іЙјЁөДЦЪКэКЗЈЁ Ј©
AЈ®98·Ц BЈ®95·Ц CЈ®94·Ц DЈ®90·Ц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁ№уЦЭБщЕМЛ®ҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
ИзНјЈ¬ФЪЎчABCЦРЈ¬АыУГіЯ№жЧчНјЈ¬»ӯіцЎчABCөДНвҪУФІ»тДЪЗРФІЈЁИОСЎТ»ёцЈ®І»РҙЧч·ЁЈ¬ұШРлұЈБфЧчНјәЫјЈЈ©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁ№уЦЭБщЕМЛ®ҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
ФЪЎчABCЦРЈ¬өгDКЗABұЯөДЦРөгЈ¬өгEКЗACұЯөДЦРөгЈ¬Б¬ҪУDEЈ¬ИфBC=4Ј¬ФтDE=ЎЎ ЎЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁёЈҪЁЖОМпҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
ИзНјЈ¬ABКЗЎСOөДЦұҫ¶Ј¬CКЗЎСOЙПөДТ»өгЈ¬№эөгAЧчADЎНCDУЪөгDЈ¬Ҫ»ЎСOУЪөгEЈ¬ЗТ =
= Ј®
Ј®
ЈЁ1Ј©ЗуЦӨЈәCDКЗЎСOөДЗРПЯЈ»
ЈЁ2Ј©ИфtanЎПCAB= Ј¬BC=3Ј¬ЗуDEөДіӨЈ®
Ј¬BC=3Ј¬ЗуDEөДіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁёЈҪЁДПЖҪҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ПВБРГҝЧйКэ·ЦұрұнКҫИэёщДҫ°фөДіӨЈ¬Ҫ«ЛьГЗКЧОІБ¬ҪУәуЈ¬ДЬ°ЪіЙИэҪЗРОөДТ»ЧйКЗЈЁЎЎЎЎЈ©
AЈ®1Ј¬2Ј¬1 BЈ®1Ј¬2Ј¬2 CЈ®1Ј¬2Ј¬3 DЈ®1Ј¬2Ј¬4
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com