
| A. | (0,-2) | B. | (-2,0) | C. | (0,2) | D. | (2,0) |
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们可以计算出
我们可以计算出查看答案和解析>>
科目:初中数学 来源: 题型:填空题
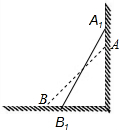 如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com