练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．若一个直角三角形的两边长分别为3和4，则第三边长的平方是（　　）
    A．7B．14C．25D．7或25

    分析 分两种情况：①当3和4为两条直角边长时；②当4为斜边长时；由勾股定理求出第三边长的平方即可．

    解答 解：分两种情况：
    ①当3和4为两条直角边长时，
    由勾股定理得：第三边长的平方=斜边长的平方=32+42=25；
    ②当4为斜边长时，
    第三边长的平方=42-32=7；
    综上所述：第三边长的平方是7或25；
    故选：D．

    点评 本题考查了勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键，注意分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．平行四边形ABCD中，若∠A+∠B=3∠C，则∠A=60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

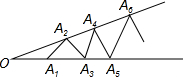    6．如图，已知点A1、A2、A3、A4…是∠O两边上的点，且O A1=A1 A2=A2 A3=A3 A4=A4 A5=…，从左向右数，恰好只能作出4个等腰三角形，请问∠O=18°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．纳米（nm）是一种长度单位，1nm为十亿分之一米，则1nm=10-9m，人体中一种细胞的直径约为1560nm，把1560nm用科学记数法可以表示为1.56×10-6m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

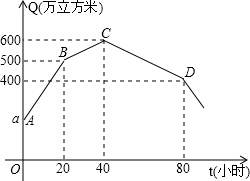    10．今年开春干旱，甲水库蓄水量降到了正常水位的最低值a，为灌溉需要，由乙水库向甲水库均速供水20小时后，甲水库打开了一个排灌闸为农田匀速灌溉，又经过20小时，甲水库打开另一个排灌闸同时灌溉，再经过40小时，乙水库停止供水，已知甲水库两个排灌闸每小时的灌溉速量相同，图中的折线表示甲水库蓄水量Q（万m3）与时间t（h）之间的函数关系，有以下四种说法：
    ①整个过程中，甲水库最大的蓄水量为600万m3
    ②乙水库向甲水库每小时供水10万m2
    ③甲水库一个排灌闸每小时的灌溉量是15万m3
    ④甲水库的正常水位的最低值a等于200（万m3）
    其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．对于题目：“化简并求值：$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$，其中a=2．”甲、乙两人的解答不同，
    甲的解答是：$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$=$\frac{1}{a}$+$\sqrt{{（\frac{1}{a}-a）}^{2}}$=$\frac{1}{a}$+$\frac{1}{a}$-a=$\frac{2}{a}$-a=$\frac{2}{2}$-2=-1；
    乙的解答是：$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$=$\frac{1}{a}$+$\sqrt{{（a-\frac{1}{a}）}^{2}}$=$\frac{1}{a}$+a-$\frac{1}{a}$=a=2．
    谁的解答是错误的？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．因式分解：a2-a=a（a-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列四个数中，比0小的数是（　　）
    A．1B．$\sqrt{3}$C．πD．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．点P为反比例函数y=$\frac{4}{x}$图象上一点，若P点的横坐标为2，则OP与x轴的正半轴夹角等于（　　）
    A．30°B．45°C．60°D．75°

    查看答案和解析>>

    同步练习册答案