
����Ŀ����ֱ֪��y=kx+3��k��0���ֱ�x�ᡢy����A��B���㣬�߶�OA����һ����P��ԭ��O���A�˶����ٶ�Ϊÿ��1����λ���ȣ�����P��x��Ĵ��߽�ֱ��AB�ڵ�C�����˶�ʱ��Ϊt�룮
��1����k=��1ʱ���߶�OA������һ����Q�ɵ�A���O�˶��������P����ͬ�ٶ�ͬʱ����������P�����Aʱ����ͬʱֹͣ�˶�����ͼ1����
��ֱ��д��t=1��ʱC��Q��������ꣻ
������Q��C��AΪ��������������AOB���ƣ���t��ֵ��
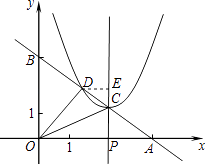
��2���� ![]() ʱ������CΪ�����������y=��x+m��2+n��ֱ��AB����һ����ΪD����ͼ2����
ʱ������CΪ�����������y=��x+m��2+n��ֱ��AB����һ����ΪD����ͼ2����
����CD�ij���
�����COD��OC���ϵĸ�Ϊh����tΪ��ֵʱ��h��ֵ���
���𰸡�
��1��
�⣺��C��1��2����Q��2��0��
��������ã�P��t��0����C��t����t+3����Q��3��t��0����
������������ۣ�
����һ������AQC�ס�AOBʱ����AQC=��AOB=90�㣬
��CQ��OA��
��CP��OA��
���P���Q�غϣ�OQ=OP��
��3��t=t��
��t=1.5��
���ζ�������ACQ�ס�AOBʱ����ACQ=��AOB=90�㣬
��OA=OB=3��
���AOB�ǵ���ֱ�������Σ�
���ACQҲ�ǵ���ֱ�������Σ�
��CP��OA��
��AQ=2CP��
��t=2����t+3����
��t=2��
������������t��ֵ��1.5���2��
��2��
��������ã�C��t���� ![]() ����
����
����CΪ����������߽���ʽ��y= ![]() ��
��
�� ![]() ��
��
����x��t��2+ ![]() ��x��t��=0��
��x��t��=0��
�ࣨx��t����x��t+ ![]() ��=0��
��=0��
��� ![]() ��
��
����D��DE��CP�ڵ�E�����DEC=��AOB=90�㣬
��DE��OA��
���EDC=��OAB��
���DEC�ס�AOB��
�� ![]() ��
��
��AO=4��AB=5��DE= ![]() ��
��
��CD= ![]() ��
��
�ڡ� ![]() ��CD���ϵĸ�=
��CD���ϵĸ�= ![]() ��
��
�� ![]() ��
��
��S��CODΪ��ֵ��
ҪʹOC���ϵĸ�h��ֵ���ֻҪOC��̣���Ϊ��OC��ABʱOC��̣�
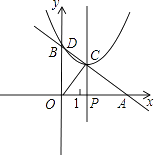
��ʱOC�ij�Ϊ ![]() ����BCO=90�㣬
����BCO=90�㣬
�ߡ�AOB=90�㣬
���COP=90�㩁��BOC=��OBA��
�֡�CP��OA��
��Rt��PCO��Rt��OAB��
�� ![]() ��OP=
��OP= ![]() ��
��
��t= ![]() ��
��
�൱tΪ ![]() ��ʱ��h��ֵ���
��ʱ��h��ֵ���
����������1����������ɵã���������õ�����t�����꣮�����������ν�𣬴Ӷ��õ��𰸣���2�����Ե�CΪ����������ߣ���ù���t�ĸ������ɹ���D��DE��CP�ڵ�E�����DEC=��AOB=90�㣬���ɡ�DEC�ס�AOB�Ӷ���ã��������������COD�����Ϊ��ֵ������Rt��PCO��Rt��OAB�����߶α�����tΪ ![]() ʱ��h���
ʱ��h���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������װ��3�������2��������Щ�����״����С���ʵ���ȫ��ͬ���ڿ�������������£�����Ӵ�����ͬʱ����2��������2�������ɫ��ͬ�ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У���B=90�㣬��AB�ϵ�һ��OΪԲ�ģ���OAΪ�뾶��Բ��AC�ڵ�D����AB�ڵ�E�� 
��1����֤��ACAD=ABAE��
��2�����BD�ǡ�O�����ߣ�D���е㣬E��OB���е㣬��BC=2ʱ����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ8cm��E��F��G�ֱ���AB��CD��DA�ϵĶ��㣬��AE=BF=CG=DH.
��1����֤���ı���EFGH�������Σ�
��2���ж�ֱ��EG�Ƿ�ijһ���㣬˵�����ɣ�
��3�����ı���EFGH�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=��2x������P����2��a������P����y��ĶԳƵ�P���ڷ��������� ![]() ��k��0����ͼ���ϣ�
��k��0����ͼ���ϣ� 
��1����a��ֵ��
��2��ֱ��д����P������ꣻ
��3�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʦΪ���˽�ѧ�����÷����������ǰһ�챾���С�Ů�����Դ���������ͳ�ƣ������Ƴ�����Ƶ���ֲ�����ͼ��ͼ1����
��1�������ͼ1���ش��������⣺
����������ѧ�������Դ�����5�ε��������ˡ�Ů�����ˣ�
���С�Ů�����Դ�������λ���ֱ����κ��Σ�
��2��ͨ������ʦ�Ĺ������ڶ���ķ��Դ�����ǰһ���������ӣ�ȫ��Դ����仯������������ͳ��ͼ��ͼ2��ʾ����ڶ��췢�Դ�������3�ε�ѧ��������ȫ�����ӵķ����ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���Rt��ABC�У���C=90�㣬AC=1������C��ֱ��l��AB��F��l�ϵ�һ�㣬��AB=AF�����F��ֱ��BC�ľ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ�ڵ�A��B��m+2��0����y���ཻ�ڵ�C����D�ڸ��������ϣ�����Ϊ��m��c�������A�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD�ǡ�O���ң�AB��ֱ������CD��AB������AC��AD��OD������AC=CD������B�����߽�CD���ӳ�����E�� 
��1����֤��DAƽ�֡�CDO��
��2����AB=12����ͼ����Ӱ���ֵ��ܳ�֮�ͣ��ο����ݣ���=3.1�� ![]() =1.4��
=1.4�� ![]() =1.7��
=1.7��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com