
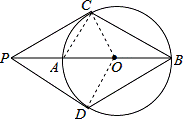
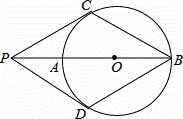
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
 其中正确的个数为( )
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
A
解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,∴∠PCO=90°,
在△PCO和△PDO中, ,∴△PCO≌△PDO(SSS),∴∠PCO=∠PDO=90°,
,∴△PCO≌△PDO(SSS),∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,故此选项正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中, ,∴△CPB≌△DPB(SAS),
,∴△CPB≌△DPB(SAS),
∴BC=BD,∴PC=PD=BC=BD,∴四边形PCBD是菱形,故此选项正确;
(3)连接AC,
∵PC=CB,∴∠CPB=∠CBP,∵AB是⊙O直径,∴∠ACB=90°,
在△PCO和△BCA中,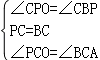 ,∴△PCO≌△BCA(ASA),
,∴△PCO≌△BCA(ASA),
∴AC=CO,∴AC=CO=AO,∴∠COA=60°,∴∠CPO=30°,
∴CO= PO=
PO= AB,∴PO=AB,故此选项正确;
AB,∴PO=AB,故此选项正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,∴∠PDB=120°,故此选项正确;故选:A.


科目:初中数学 来源: 题型:
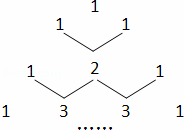
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4= .
查看答案和解析>>
科目:初中数学 来源: 题型:
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C. (x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com