
����Ŀ����֪����������y=![]() ��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��1����A��4��n����B��n+![]() ��3�������������ı���ʽ��
��3�������������ı���ʽ��
��2����m=1��
�ٵ�x2=1ʱ��ֱ��д��y1��ȡֵ��Χ��
�ڵ�x1��x2��0��p=![]() ��q=
��q=![]() �����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
�����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
��3������A��B�����ֱ��y=x+2��y�ύ�ڵ�C������BO���ǡ�COB�����ΪS����![]() ��S��1����m��ȡֵ��Χ��
��S��1����m��ȡֵ��Χ��
���𰸡���1��y=![]() ����2���ٵ�0��x1��1ʱ��y1��1����x1��0ʱ��y1��0����p��q������������3��
����2���ٵ�0��x1��1ʱ��y1��1����x1��0ʱ��y1��0����p��q������������3��![]() ��m��3��-1��m��-
��m��3��-1��m��-![]()
��������
��1������A��B��������뷴������������ʽ�У����������鼴�ɵó����ۣ�
��2���ȵó���������������ʽ��
���ȵó�x1=![]() ���ٷ�����������ۼ��ɵó����ۣ�
���ٷ�����������ۼ��ɵó����ۣ�
���ȱ�ʾ��y1=![]() ��y2=
��y2=![]() �������ó�p=
�������ó�p=![]() ���������������ɵó����ۣ�
���������������ɵó����ۣ�
��3������m��ʾ��x2=-1+![]() ���������C���꣬������x2��ʾ��S���ٷ����������
���������C���꣬������x2��ʾ��S���ٷ����������![]() ��S��1ȷ����x2�ķ�Χ�����ɵó�-1+
��S��1ȷ����x2�ķ�Χ�����ɵó�-1+![]() �ķ�Χ�����ɵó�m�ķ�Χ��
�ķ�Χ�����ɵó�m�ķ�Χ��
�⣺��1����A��4��n����B��n+![]() ��3���ڷ���������y=
��3���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��4n=3��n+![]() ��=m��
��=m��
��n=1��m=4��
�������������ı���ʽΪy=![]() ��
��
��2����m=1��
�������������ı���ʽΪy=![]() ��
��
����ͼ1����B��x2��y2���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
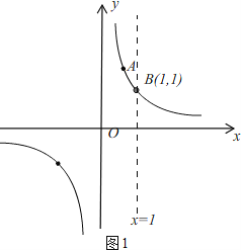
��y2=1��
��B��1��1����
��A��x1��y1���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��y1=![]() ��
��
��x1=![]() ��
��
��x1��x2��x2=1��
��x1��1��
��0��x1��1ʱ��y1��1��
��x1��0ʱ��y1��0��
��p��q�����ɣ�������������y=![]() ��ͼ����A��x1��y1����B��x2��y2����
��ͼ����A��x1��y1����B��x2��y2����
��y1=![]() ��y2=
��y2=![]() ��
��
��p=![]() =
=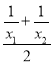 =
=![]() ��
��
��q=![]() ��
��
��p-q=![]() -
-![]() =
=![]() =
=![]() ��
��
��x1��x2��0��
����x1+x2��2��0��x1x2��0��x1+x2��0��
��![]() ��0��
��0��
��p-q��0��
��p��q��
��3������B��x2��y2����ֱ��AB��y=x+2�ϣ�Ҳ���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��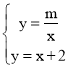 ����ã�x=-1
����ã�x=-1![]() ��
��
��x1��x2��
��x2=-1+![]()
��ֱ��AB��y=x+2��y���ཻ�ڵ�C��
��C��0��2����
��m��0ʱ����ͼ2��

��A��x1��y1����B��x2��y2����x1��x2����
����B��������0��
����x2��0
��S=![]() OCx2=
OCx2=![]() ��2��x2=x2��
��2��x2=x2��
��![]() ��S��1��
��S��1��
��![]() ��x2��1��
��x2��1��
��![]() ��-1+
��-1+![]() ��1��
��1��
��![]() ��m��3��
��m��3��
��m��0ʱ����ͼ3����A��x1��y1����B��x2��y2����x1��x2����
����B�ĺ�����С��0��

����x2��0
��S=![]() OC|x2|=-
OC|x2|=-![]() ��2��x2=-x2��
��2��x2=-x2��
��![]() ��S��1��
��S��1��
��![]() ��-x2��1��
��-x2��1��
��-1��x2��-![]() ��
��
��-1��-1+![]() ��-
��-![]() ��
��
��-1��m��-![]() ��
��
������![]() ��S��1ʱ��m��ȡֵ��ΧΪ
��S��1ʱ��m��ȡֵ��ΧΪ![]() ��m��3��-1��m��-
��m��3��-1��m��-![]() ��
��


 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���36000Ԫ�����ס���������Ʒ�����������6000Ԫ�����м�����Ʒÿ������120Ԫ���ۼ�138Ԫ��������Ʒÿ������100Ԫ���ۼ�120Ԫ��
��1�����̳������ס���������Ʒ�����ټ���
��2���̳��ڶ�����ԭ���۹����ס���������Ʒ������������Ʒ�ļ������䣬������������Ʒ�ļ����ǵ�һ�ε�2����������Ʒ��ԭ�ۼ۳��ۣ���������Ʒ�������ۣ���������Ʒ������ϣ�Ҫʹ�ڶ��ξ�Ӫ�����������8160Ԫ��������Ʒ����ۼ�Ϊÿ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ����S������ABCD=4+
����S������ABCD=4+![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��

A.�٢ۢ� B���٢ڢ� C���ۢܢ� D���٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ������
ij��������![]() Ԫ/
Ԫ/ ![]() �ijɱ��۹�����ij��Ʒ
�ijɱ��۹�����ij��Ʒ![]() �����г�Ԥ�⣬�ò�Ʒ�����ۼ�
�����г�Ԥ�⣬�ò�Ʒ�����ۼ�![]() ��Ԫ/
��Ԫ/ ![]() ���뱣��ʱ��
���뱣��ʱ��![]() ���죩�ĺ�����ϵΪ
���죩�ĺ�����ϵΪ![]() ��������������Ʒƽ��ÿ�콫���
��������������Ʒƽ��ÿ�콫���![]() �����⣬������ÿ�챣�������Ʒ�ķ���Ϊ
�����⣬������ÿ�챣�������Ʒ�ķ���Ϊ![]() Ԫ����֪�ò�Ʒÿ�������������
Ԫ����֪�ò�Ʒÿ�������������![]() ����������ϣ��ͨ��������Ʒ��������
����������ϣ��ͨ��������Ʒ��������![]() Ԫ����������Ӧ�ڱ���ò�Ʒ������ʱһ����������
Ԫ����������Ӧ�ڱ���ò�Ʒ������ʱһ����������
С����˼·�����
�������ȹ�ϵ�ǣ�
���ۼ�![]() ����
����![]() �ɱ���
�ɱ���![]() ����
����![]() �������
�������![]() ������
������
�⣺��������Ӧ�ڱ���ò�Ʒ![]() ��ʱһ���������ɻ���
��ʱһ���������ɻ���![]() Ԫ��
Ԫ��
�����������ȹ�ϵ��
��![]() ��
��
��������̣���![]() ��
�� ![]() ��
��
��![]() ʱ��
ʱ�� ![]() ���������⣬��ȥ����
���������⣬��ȥ����
��![]() ʱ��
ʱ�� ![]() ��
��
��������Ӧ�ڱ���ò�Ʒ![]() ��ʱһ���������ɻ���
��ʱһ���������ɻ���![]() Ԫ��
Ԫ��
��ѧ��ʦ������
��ѧ��ʦ��С���Ľ���л���һ�����ߣ�������һ����![]() ����
����
��Ĺ۵㼰����
��![]() ����ָ��С�������ԭ��
����ָ��С�������ԭ��
��![]() �����¸�����ȷ�Ľ����̣�
�����¸�����ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����������������������AB��CD��AD��BC����AB=CD��AD=BC����AO=CO��BO=DO����AB��CD��AD=BC������һ�����ж�����ı�����ƽ���ı��ε���������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y1��![]() ��ͼ����һ�κ���y2��ax+b��ͼ���ڵ�A��1��4���͵�B��m����2����
��ͼ����һ�κ���y2��ax+b��ͼ���ڵ�A��1��4���͵�B��m����2����
��1���������������Ĺ�ϵʽ��
��2���۲�ͼ��д��ʹ��y1��y2�������Ա���x��ȡֵ��Χ��
��3�������C���A����x��Գƣ�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
(1)(![]() )��2��(��2)0+(��0.2)2018��(��5)2018��
)��2��(��2)0+(��0.2)2018��(��5)2018��
(2)����ʽ�˷���ʽ���㣺1012��1��
(3)(x2y+2x2y��y3)��y��(y+2x)(2x��y)��
(4)�Ȼ�������ֵ��(a��2b)2+(a��b)(a+b)��2(a��3b)(a��b)�����У�a��1��b����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
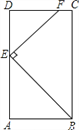
����Ŀ����ͼ���ھ���ABCD�У�AB=3��AD=6����E��AD���ϣ���AE=4��EF��BE��CD�ڵ�F��
��1����֤����ABE�ס�DEF��
��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�߳�Ϊ3������AC��AEƽ����CAD����BC���ӳ����ڵ�E��FA��AE����CB�ӳ����ڵ�F����EF�ij�Ϊ__________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com