练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．

    【答案】6

    【解析】试题分析：利用正方形的性质和勾股定理可得AC的长，由角平分线的性质和平行线的性质可得∠CAE=∠E，易得CE=CA，由FA⊥AE，可得∠FAC=∠F，易得CF=AC，可得EF的长．

    ∵四边形ABCD为正方形，且边长为3， ∴AC=3， ∵AE平分∠CAD， ∴∠CAE=∠DAE，

    ∵AD∥CE， ∴∠DAE=∠E， ∴∠CAE=∠E， ∴CE=CA=3， ∵FA⊥AE，

    ∴∠FAC+∠CAE=90°，∠F+∠E=90°， ∴∠FAC=∠F， ∴CF=AC=3，

    ∴EF=CF+CE=3+3=6

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列说法错误的是（ ）
    A.数轴上表示﹣2的点与表示+2的点的距离是2
    B.数轴上原点表示的数是0
    C.所有的有理数都可以用数轴上的点表示出来
    D.最大的负整数是﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知方程ax+12=0的解是x=3，求满足关于y的不等式（a+2）y＜7的最小整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

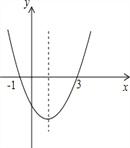
    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列6个结论正确的有________个.

    ①ac<0；②2a+b=0；③4a+2b+c>0；④对于任意x均有ax2+bx≥a+b；⑤3a+c=0；⑥b+2c<0；⑦当x>1时，y随着x的增大而减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB∥CD，∠EBF=2∠ABE，∠EDF=2∠CDE，则∠E与∠F之间满足的数量关系是（ ）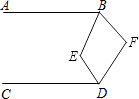

    A.∠E=∠F
    B.∠E+∠F=180°
    C.3∠E+∠F=360°
    D.2∠E﹣∠F=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.﹣12﹣8=﹣4
    B.﹣5+4=﹣9
    C.﹣1﹣9=﹣10
    D.﹣32=9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题6分）甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．

    （1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；

    （2）若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一副三角尺叠放的示意图，则∠α的度数为（ ）
    A.75°
    B.45°
    C.30°
    D.15°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E．若∠C=60°，∠BED=70°．求∠ABC和∠BAC的度数．

    查看答案和解析>>

    同步练习册答案