Question

【题目】如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．
（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4 ，求四边形AEDF的周长．

Answer 1

【答案】
（1）证明：∵E，D，F分别是边AB，BC，AC的中点，

∴DE∥AF且DE= =AF，

∴四边形AEDF为平行四边形，

同理可得，DF∥AB且DF= ，

∵AB=AC，

∴DE=DF，

∴四边形AEDF是菱形

（2）解：连接AD，

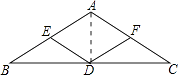
∵AB=AC，D为BC的中点，

∴AD⊥BC，BD=BC= ，

∴AE= = =4，

∵四边形AEDF是菱形，

∴四边形AEDF的周长为4×4=16．

【解析】（1）由AB=AC利用中位线的性质可得DE=DF，四边形AEDF为平行四边形，由邻边相等的平行四边形是菱形证得结论；（2）首先由等腰三角形的性质“三线合一”得AD⊥BC，BD=BC= ，由锐角三角函数定义得AE，易得四边形AEDF的周长．
【考点精析】本题主要考查了等腰三角形的性质和三角形中位线定理的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．