
【题目】问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC的度数和等边三角形ABC的边长.
,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=![]() ,PB=
,PB=![]() ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.
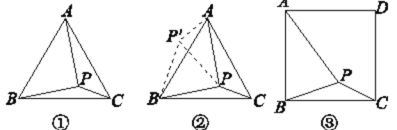
【答案】(1)∠AP′B=150°,∠BPC=∠AP′B=150°,等边三角形ABC的边长为![]() ;(2)∠BPC=135°,正方形ABCD的边长为
;(2)∠BPC=135°,正方形ABCD的边长为![]() .
.
【解析】
根据旋转得出AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=
,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=![]() ,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=
,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=![]() ,P′M=
,P′M=![]() ,根据勾股定理即可求出答案;
,根据勾股定理即可求出答案;
(2)求出∠BEP=![]() (180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(1)∵等边△ABC,
∴∠ABC=60°,
将△BPC绕点B逆时针旋转60°得出△ABP′,
∴AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,
,∠PBC=∠P′BA,∠AP′B=∠BPC,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=![]() ,∠BP′P=60°,
,∠BP′P=60°,
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,
∴∠BPC=∠AP′B=90°+60°=150°,
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=![]() ,
,
由勾股定理得:P′M=![]() ,
,
∴AM=1+![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
故答案为:150°,![]() .
.
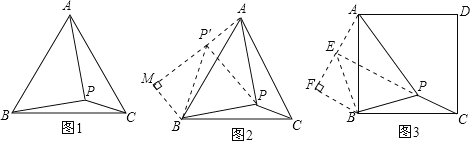
(2)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=![]() (180°-90°)=45°,
(180°-90°)=45°,
由勾股定理得:EP=2,
∵AE=1,AP=![]() ,EP=2,
,EP=2,
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°,
过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:∠BPC的度数是135°,正方形ABCD的边长是![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
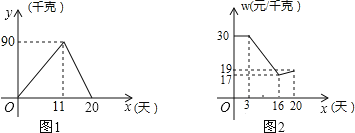
【题目】小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.
(1)观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为 ;
当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .
(2)试求出第11天的销售金额;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
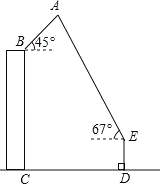
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且BF=DE,连接AE,AF,EF.

(1)判断△ABF与△ADE有怎样的关系,并说明理由;
(2)求∠EAF的度数,写出△ABF可以由△ADE经过怎样的图形变换得到;
(3)若BC=6,DE=2,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】均衡化验收以来,乐陵每个学校都高楼林立,校园环境美如画,软件、硬件等设施齐全,小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走6 米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°,已如A点离地面的高度AB=4米,∠BCA=30°,且B、C、D 三点在同一直线上.
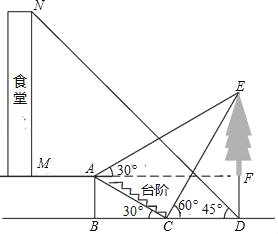
(1)求树DE的高度;
(2)求食堂MN的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
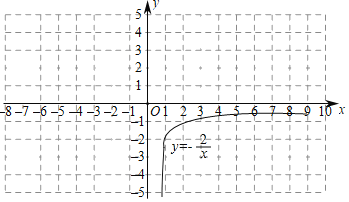
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2,﹣
﹣2,﹣![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和B,与y轴的正半轴交于点C,下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0,其中正确的个数为( )
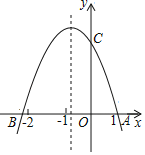
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com