
分析 ①先根据已知利用SAS判定△ABM≌△BCN,再根据全等三角形的性质求得∠AQN=∠ABC=60°,②根据三角形全等得出∠M=∠N,根据求出∠M+∠CAM=∠ACB=60°,推出∠N+∠NAQ=60°,即可得出答案.
解答 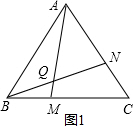 解:①如图1,点M在线段BC上,
解:①如图1,点M在线段BC上,
∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC,
在△AMB和△BNC中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠C}\\{BM=CN}\end{array}\right.$,
△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC-∠MAB=60°-∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°-∠ANB-∠MAN,
∠AQN=180°-(∠ANB+∠MAN),
=180°-120°=60°,
②如图2,点M在BC的延长线上,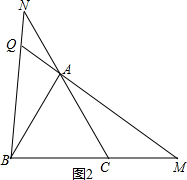 ∵△BCN≌△ABM,
∵△BCN≌△ABM,
∴∠M=∠N,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠M+∠CAM=∠ACB=60°,
∵∠M=∠N,∠CAM=∠NAQ,
∴∠N+∠NAQ=60°,
∴∠BQM=∠N+∠NAQ=60°,
∴∠AQN=120°.
综上所述:∠AQN的度数为60°或120°.
故答案为:60°或120°.
点评 本题考查了等边三角形性质,全等三角形的性质和判定,三角形的外角性质,熟练掌握全等三角形的判定和性质是解题的关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全市七年级学生是总体 | |
| B. | 2000名学生是总体的一个样本 | |
| C. | 每名学生的视力情况是总体的一个个体 | |
| D. | 样本容量是2000名 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.
如图,已知E、F分别是?ABCD的边BC、AD上的点,且BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式-$\frac{{x}^{2}}{3}$的系数-3 | |
| B. | 单项式$\frac{2{π}^{2}a{b}^{4}}{3}$的指数是7 | |
| C. | 多项式x3y-2x2+3是四次三项式 | |
| D. | 多项式x3y-2x2+3的项分别为x3y,2x2,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com