已知:一次函数y=x+4的图象与二次函数y=x2+bx+c的图象都经过点Q(-1,m)和点A(n,0),二次函数图象的顶点为M.
求:(1)这个二次函数的解析式.
(2)∠OQM的度数.

解:(1)把(-1,m)、(n,0)代入一次函数y=x+4中,得
m=3,n=-4,
再把(-1,3)(-4,0)代入二次函数y=x
2+bx+c中,得
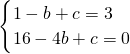
,
解得
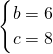
,
∴二次函数的解析式是y=x
2+6x+8;
(2)∵y=x
2+6x+8,如右图,
∴此函数顶点坐标是(-3,-1),
∵Q(-1,3),O(0,0),M(-3,-1),
∴OQ=

,OM=

,QM=2

,
∴OQ
2+OM
2=QM
2,OQ=OM,
∴△OMQ是等腰直角三角形,
∴∠OQM=45°.
分析:(1)先把(-1,m)、(n,0)代入一次函数y=x+4中,易求m、n的值,再把Q、A点的坐标代入二次函数,可得关于b、c的二元一次方程组,解即可求b、c,进而可得二次函数解析式;
(2)根据(1)中所求二次函数解析式,结合顶点的计算公式,易求M的坐标,利用两点之间的距离公式,易求OQ、OM、QM的长,进而可知OQ
2+OM
2=QM
2,OQ=OM,易知△OMQ是等腰直角三角形,那么∠OQM=45°.
点评:本题考查了待定系数法求函数解析式、两点之间的距离公式,解题的关键是理解点与函数解析式之间的关系,以及熟练掌握二次函数顶点的计算公式、并会画出草图.

 解:(1)把(-1,m)、(n,0)代入一次函数y=x+4中,得
解:(1)把(-1,m)、(n,0)代入一次函数y=x+4中,得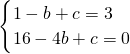 ,
,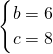 ,
, ,OM=
,OM= ,QM=2
,QM=2 ,
,
