
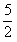 以其顶点为中心旋转180°后,与x轴正半轴交于A点,与y 轴交于B点,在第二象限内存在一点C(a,1),顺次连接A、B、C、O得到一个四边形,过B 点作直线l将此图形分成面积相等的两部分,求:
以其顶点为中心旋转180°后,与x轴正半轴交于A点,与y 轴交于B点,在第二象限内存在一点C(a,1),顺次连接A、B、C、O得到一个四边形,过B 点作直线l将此图形分成面积相等的两部分,求:解:(1)将y=x2+x+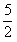 配方后得: 配方后得: ∴旋转后的抛物线解析式为:y=-(x+ 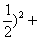  即:y=-x2-x+2。 |
|
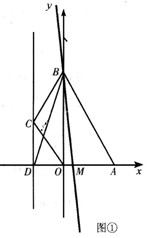
| (2)∵y=-x2-x+2, ∴A(1,0),B(0,2) ①当-1<a<0时,如图①,过C作CD∥y轴交x 轴于D,连接BD, S△BCO=S△BDO, 则S△BDA=S四边形BCOA,取DA中点M,作直线BM,直线BM即为所求 ∵C(a,1), ∴D(a,0) ∵A(1,0), ∴线段DA中点M的坐标为 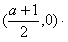 设直线l的解析式为y=kx+2, ∴0=k· 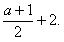 ∴  ∴直线l的解析式为y= 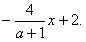 。 。 |
 |
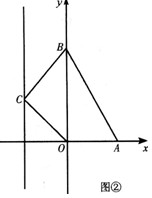
| ②当a=-1时,如图②, 用①的方法操作,可知y轴为符合题意的直线l 即直线l的解析式为x=0。 |
 |
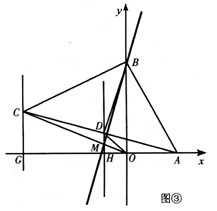
| ③当a<-1时,如图③, 连接CA并取中点D,连接BD、DO, ∴S四边形BCDO=S四边形BAOD 过D点作DH//y轴,交OC于M,交x轴于H,作直线BM ∴S△BDO=S△BMO, 即S△BCM=S四边形BMOA 即直线BM是符合题意的直线l 过C点作CG∥y轴,交x轴于G, ∴H为GA的中点, ∵G(a,0),A(1,0) ∴ 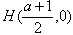 设M坐标为(xm,ym),则xm= 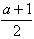 设直线OC的解析式为y= 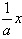 M在OC上 ∴ 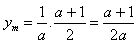 ∴M坐标为 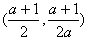 设直线l的解析式为y=kx+2 ∴  ∴ 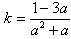 ∴直线l的解析式为y= 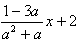 综上所述:当-1<a<0时,直线l的解析式为y= 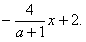 当a=-1时,直线l的解析式为x=0 当a<-1时,直线l的解析式为y=  |
 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
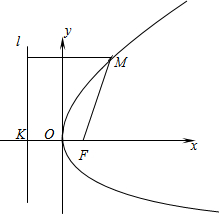 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题.| p |
| 2 |
| p |
| 2 |
(x-
|
| p |
| 2 |
(x-
|
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 标准方程 | 交点坐标 | 准线方程 | ||||
| y2=2px(p>0) | (
|
x=-
| ||||
| y2=-2px(p>0) | (-
|
x=
| ||||
| x2=2py(p>0) | (0,
|
y=-
| ||||
| x2=-2py(p>0) | (0,-
|
y=-
|
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
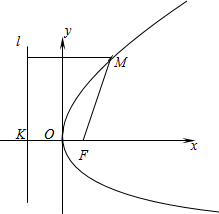 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题. ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.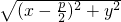 ,d=|x+
,d=|x+ |∴
|∴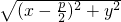 =|x+
=|x+ |
| ,0),它的准线方程是x=-
,0),它的准线方程是x=- .
.| 标准方程 | 交点坐标 | 准线方程 |
| y2=2px(p>0) | (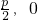 ) ) | x=- |
| y2=-2px(p>0) | (-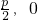 ) ) | x= |
| x2=2py(p>0) | (0, ) ) | y=- |
| x2=-2py(p>0) | (0,- ) ) | y=- |
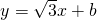 经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.
经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com