
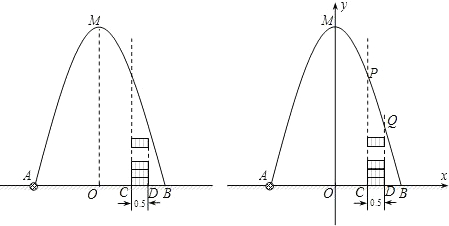
 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.| 5 |
| 4 |
| 5 |
| 4 |
| 15 |
| 4 |
| 3 |
| 2 |
| 35 |
| 16 |
| 15 |
| 4 |
| 3 |
| 2 |
| 35 |
| 16 |
| 15 |
| 4 |
| 35 |
| 16 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).| 35 |
| 16 |
| 35 |
| 16 |
| 9 |
| 5 |
| 9 |
| 5 |
| 94 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(云南昭通) 题型:解答题
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).

(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com