
| 鲢鱼 | 草鱼 | 青鱼 | |
| 每辆汽车载鱼量(吨) | 8 | 6 | 5 |
| 每吨鱼获利(万元) | 0.25 | 0.3 | 0.2 |
分析 (1)设装运鲢鱼的车辆为x辆,装运草鱼的车辆为y辆,则由(20-x-y)辆汽车装运青鱼,由20辆汽车的总运输量为120吨建立等式就可以求出结论;
(2)根据建立不等装运每种鱼的车辆都不少于2辆,列出不等式组求出x的范围,设此次销售所获利润为w元,
w=0.25x×8+0.3(-3x+20)×6+0.2(20-x+3x-20)×5=-1.4x+36,再利用一次函数的性质即可解答.
解答 解:(1)设装运鲢鱼的车辆为x辆,装运草鱼的车辆为y辆,则由(20-x-y)辆汽车装运青鱼,由题意,得
8x+6y+5(20-x-y)=120,
∴y=-3x+20.
答:y与x的函数关系式为y=-3x+20;
(2),根据题意,得$\left\{\begin{array}{l}{x≥2}\\{y≥2}\\{20-x-y≥2}\end{array}\right.$
∴$\left\{\begin{array}{l}{x≥2}\\{-3x+20≥2}\\{20-x+3x-20≥2}\end{array}\right.$,
解得:2≤x≤6,
设此次销售所获利润为w元,
w=0.25x×8+0.3(-3x+20)×6+0.2(20-x+3x-20)×5=-1.4x+36
∵k=-1.4<0,
∴w随x的增大而减小.
∴当x=2时,w取最大值,最大值为:-1.4×2+36=33.2(万元).
∴装运鲢鱼的车辆为2辆,装运草鱼的车辆为14辆,装运青鱼的车辆为4辆时获利最大,最大利润为33.2万元.
点评 本题考查了一次函数的解析式的运用,一次函数的性质的运用,一元一次不等式组的运用,解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:填空题
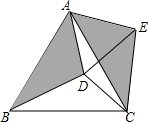 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
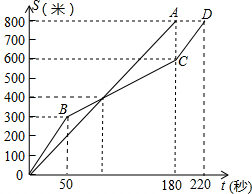 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )| A. | 甲的速度随时间的增加而增大 | B. | 乙的平均速度比甲的平均速度大 | ||
| C. | 在起跑后第180秒时,两人相遇 | D. | 在起跑后第50秒时,乙在甲的前面 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{s}{x}$=$\frac{s+50}{x+v}$ | B. | $\frac{s}{x+v}$=$\frac{s+50}{x}$ | C. | $\frac{s}{x}$=$\frac{s+50}{x-v}$ | D. | $\frac{s}{x-v}$=$\frac{s+50}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com