练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如何求22.5°的正切值，小明想了一个办法：把一张正方形纸片（正方形ABCD）按如图方式折叠，使顶点B恰好落在对角线AC上，折痕为EC．根据小明的操作通过计算可以得到tan22.5°=
    		2
    -1
    		2
    -1
    ．（保留根号）
    分析：根据题意可得∠AEB'=45°，设BE=EB'=x，则AE=
    		2
    x，AB=（
    		2
    +1）x，从而根据tan∠BCE=tan22.5°=
    BE
    BC
    =
    BE
    AB
    ，可得出答案．
    解答：解：∵四边形ABCD是正方形，
    ∴∠EAB'=45°，
    ∵∠EB'C=∠EBC=90°（折叠的性质），
    ∴∠AEB'=45°，
    设BE=EB'=x，则AE=
    		2
    x，AB=（
    		2
    +1）x，
    则tan∠BCE=tan22.5°=
    BE
    BC
    =
    BE
    AB
    =
    x
    (
    		2
    +1)x
    =
    		2
    -1．
    故答案为：
    		2
    -1．
    点评：本题考查了翻折变换的知识，解答本题的关键是发现△AEB'为等腰直角三角形，从而设出未知数，表示出有关线段求解，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•雨花台区一模）如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=5cm，D是BC边上一点，CD=3cm，点P为边AC上一动点（点P与A、C不重合），过点P作PE∥BC，交AD于点E．点P以1cm/s的速度从A到C匀速运动．
    （1）设点P的运动时间为t（s），DE的长为y（cm），求y关于t的函数关系式，并写出t的取值范围；
    （2）当t为何值时，以PE为半径的⊙E与以DB为半径的⊙D外切？并求此时∠DPE的正切值；
    （3）将△ABD沿直线AD翻折，得到△AB’D，连接B’C．如果∠ACE=∠BCB’，求t的值．

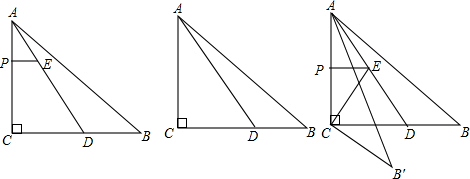
    查看答案和解析>>

    科目：初中数学 来源： 题型：

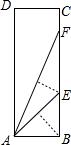    将如图的矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点E处，还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，这样就可以求出∠AFE的正切值是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=4㎝，BC=5㎝，D是BC边上一点，CD=3㎝，点P为边AC上一动点（点P与A、C不重合），过点P作PE// BC，交AD于点E．点P以1㎝/s的速度从A到C匀速运动。
    【小题1】设点P的运动时间为t（s），DE的长为y（cm），求y关于t的函数关系式，并写出的取值范围；
    【小题2】当t为何值时，以PE为半径的⊙E与以DB为半径的⊙D外切？并求此时∠DPE的正切值；
    【小题3】将△ABD沿直线AD翻折，得到△AB’D，连接B’ C．如果∠ACE=∠BCB’，求t的值．

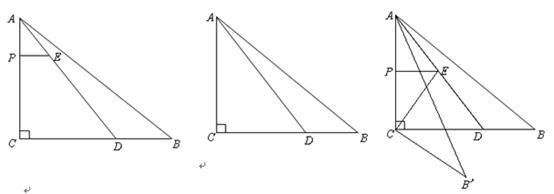
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如何求22.5°的正切值，小明想了一个办法：把一张正方形纸片（正方形ABCD）按如图方式折叠，使顶点B恰好落在对角线AC上，折痕为EC．根据小明的操作通过计算可以得到tan22.5°=________．（保留根号）

    查看答案和解析>>

    同步练习册答案