Question

【题目】如图，在正方形中， 是边上一点，连结，过点作⊥，交于点，交延长线于点，若＝12， ＝5，解答下列问题：

（1）直接写出两对相似的三角形；

（2）求的长.

Answer 1

【答案】（1）∽， ∽（2） ．

【解析】试题分析：

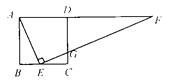
(1) 由∠ABC=∠BCD=90°，EF⊥AE可知△ABE∽△ECG；由AF∥BC可知△FDG∽△ECG；由∠AEF=∠GDF=90°，∠F=∠F可知△AEF∽△GDF；由以上相似三角形，根据相似三角形的传递性可知△ABE∽△FDG，△ABE∽△FEA，△ECG∽△FEA等. 从其中任意选取两组相似三角形作答即可.

(2) 要求线段DF的长，只要求得线段AF的长. 利用已知条件和勾股定理可以获得Rt△ABE三条边的长度；利用AD∥BC，EF⊥AE，∠ABC=90°，不难通过“两组对应角相等的两个三角形相似”判定△FEA∽△ABE. 线段AF的长度可以通过这组相似三角形对应边的比例关系求得，进而得到线段DF的长.

试题解析：

(1) △ABE∽△ECG，△FDG∽△ECG. 证明过程如下.

证明：∵∠ABC=∠BCD=90°，

∴∠BAE+∠AEB=∠CEG+∠EGC=90°，

∵EF⊥AE，

∴∠AEB+∠CEG=90°，

∴∠BAE=∠CEG.

∵∠ABE=∠ECG=90°，∠BAE=∠CEG，

∴△ABE∽△ECG.

∵四边形ABCD为正方形，

∴AD∥BC，即AF∥BC，

∴△FDG∽△ECG.

(2) ∵四边形ABCD是正方形，

∴∠B=90°，

∴△ABE是直角三角形，

∵AB=12，BE=5，

∴在Rt△ABE中， .

∵四边形ABCD是正方形，

∴AD∥BC，

∴∠DAE=∠AEB，即∠FAE=∠AEB，

∵EF⊥AE，

∴∠AEF=90°，

∵∠AEF=∠B=90°，∠FAE=∠AEB，

∴△FEA∽△ABE，

∴，

∵EA=13，BE=5，

∴，

∴，

∴.