Question

6．如图，已知抛物线y=ax²+bx（a≠0）经过A（3，0）、B（4，4）两点．
（1）抛物线的解析式为y=x²-3x；
（2）若点D、N均在此抛物线上，其中点D坐标为（2，-2），点N满足∠NBO=∠ABO，P为平面上一点，则所有满足△POD∽△NOB的点P的坐标有（-$\frac{3}{8}$，-$\frac{45}{32}$），（$\frac{45}{32}$，$\frac{3}{8}$）（点P、O、D分别与点N、O、B对应）．

Answer 1

分析 （1）利用待定系数法求二次函数解析式进而得出答案即可；
（2）根据解方程组，可得N点坐标，求出直线A′B的解析式，进而由△P₁OD∽△NOB，得出△P₁OD∽△N₁OB₁，进而求出点P₁的坐标，再利用翻折变换的性质得出另一点的坐标．

解答 解：（1）∵抛物线y=ax²+bx（a≠0）经过点A（3，0）、B（4，4），
∴$\left\{\begin{array}{l}{9a+3b=0}\\{16a+4b=4}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$．
∴抛物线的解析式是y=x²-3x．
故答案为y=x²-3x；

（2）易求直线OB的解析式为y=x，且A（3，0），
∴点A关于直线OB的对称点A'的坐标是（0，3）．
设直线A'B的解析式为y=kx+3，过点B（4，4），
∴4k+3=4，解得：k=$\frac{1}{4}$．
∴直线A'B的解析式是y=$\frac{1}{4}$x+3．
∵∠NBO=∠ABO，
∴点N在直线A'B上，
∴设点N（n，$\frac{1}{4}$n+3），又点N在抛物线y=x²-3x上，
∴$\frac{1}{4}$n+3=n²-3n，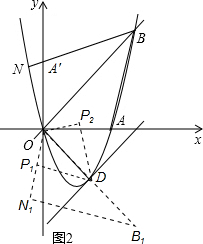
解得：n₁=-$\frac{3}{4}$，n₂=4（与B重合，不合题意，会去），
∴点N的坐标为（-$\frac{3}{4}$，$\frac{45}{16}$）．
将△NOB沿x轴翻折，得到△N₁OB₁，
则N₁（-$\frac{3}{4}$，-$\frac{45}{16}$），B₁（4，-4），
∴O、D、B₁都在直线y=-x上
如图，过D点做DP₁∥N₁B₁，
∵△P₁OD∽△NOB，
∴△P₁OD∽△N₁OB₁，
∴P₁为O N₁的中点．
∴$\frac{O{P}_{1}}{O{N}_{1}}$=$\frac{OD}{O{B}_{1}}$=$\frac{1}{2}$，
∴点P₁的坐标为（-$\frac{3}{8}$，-$\frac{45}{32}$）．
将△P₁OD沿直线y=-x翻折，可得另一个满足条件的点到x轴距离等于P₁到y轴距离，点到y轴距离等于P₁到x轴距离，
∴此点坐标为（$\frac{45}{32}$，$\frac{3}{8}$）．
综上所述，点P的坐标是（-$\frac{3}{8}$，-$\frac{45}{32}$），（$\frac{45}{32}$，$\frac{3}{8}$）．
故答案为（-$\frac{3}{8}$，-$\frac{45}{32}$），（$\frac{45}{32}$，$\frac{3}{8}$）．

点评 本题考查了待定系数法求抛物线解析式、翻折变换以及相似三角形等重要知识点．本题将初中阶段重点代数、几何知识熔于一炉，难度很大，对学生能力要求极高，具有良好的区分度，是一道非常好的中考压轴题．